《九年級(jí)數(shù)學(xué)上學(xué)期期中試題 北師大版(I)》由會(huì)員分享�,可在線閱讀,更多相關(guān)《九年級(jí)數(shù)學(xué)上學(xué)期期中試題 北師大版(I)(6頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索����。
1、九年級(jí)數(shù)學(xué)上學(xué)期期中試題 北師大版(I)
一��、選擇題(每小題3分����,共36分)
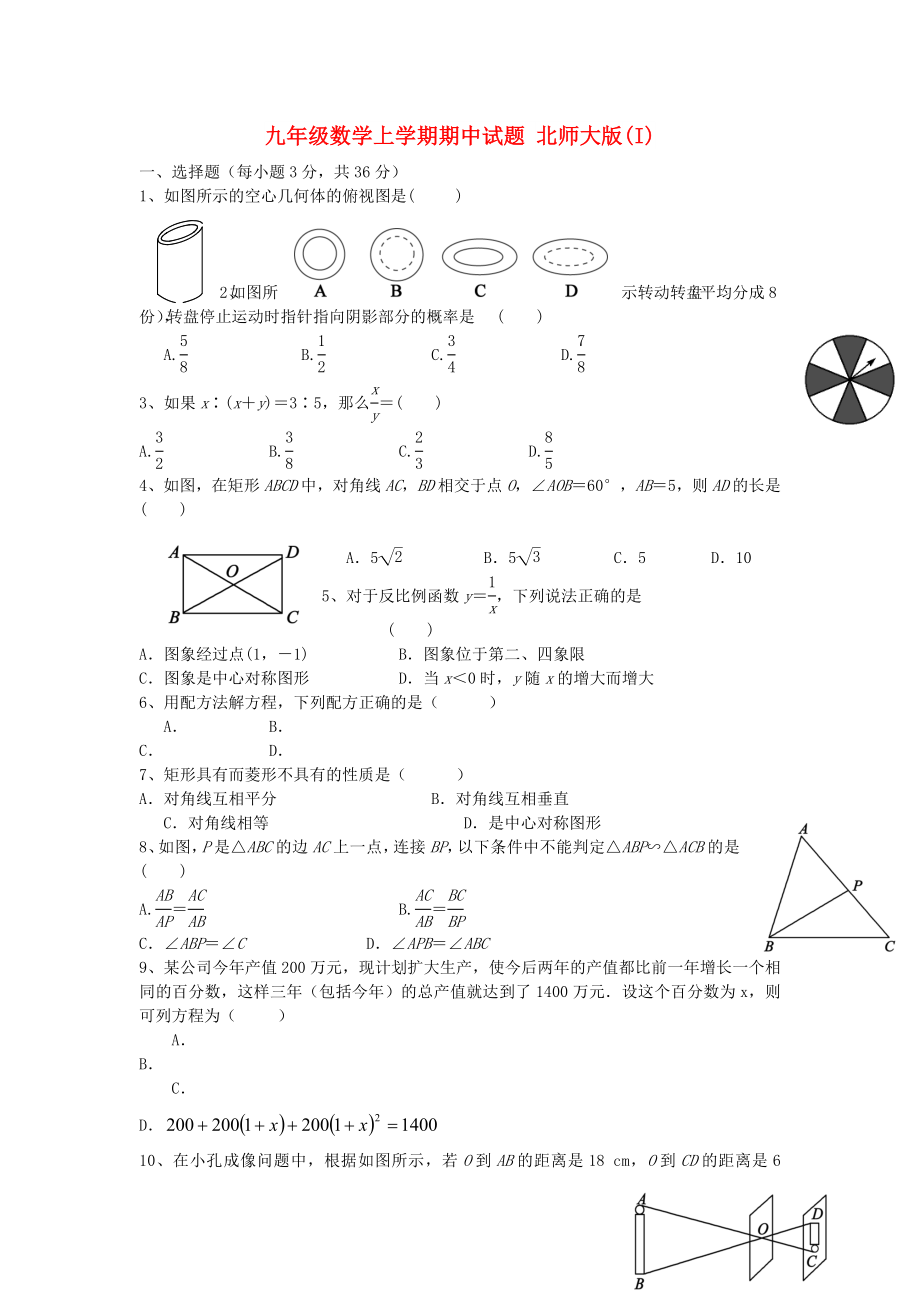
1、如圖所示的空心幾何體的俯視圖是( )
2���、如圖所示轉(zhuǎn)動(dòng)轉(zhuǎn)盤(平均分成8份)���,轉(zhuǎn)盤停止運(yùn)動(dòng)時(shí)指針指向陰影部分的概率是 ( )
A. B. C. D.
3、如果x∶(x+y)=3∶5����,那么=( )
A. B. C. D.
4、如圖,在矩形ABCD中�����,對(duì)角線AC�,BD相交于點(diǎn)O,∠AOB=60°�����,AB=5�,則AD的長是( )
A.5 B.5 C.5 D.10
5����、對(duì)于反比例函數(shù)y=,下列說法正確的是
2����、 ( )
A.圖象經(jīng)過點(diǎn)(1,-1) B.圖象位于第二����、四象限
C.圖象是中心對(duì)稱圖形 D.當(dāng)x<0時(shí),y隨x的增大而增大
6����、用配方法解方程���,下列配方正確的是( )
A. B.
C. D.
7、矩形具有而菱形不具有的性質(zhì)是( )
A.對(duì)角線互相平分 B.對(duì)角線互相垂直
C.對(duì)角線相等 D.是中心對(duì)稱圖形
8���、如圖�����,P是△ABC的邊AC上一點(diǎn)����,連接BP��,以下條件中不能判定△ABP∽△ACB的是( )
A.= B.=
3�����、
C.∠ABP=∠C D.∠APB=∠ABC
9��、某公司今年產(chǎn)值200萬元�,現(xiàn)計(jì)劃擴(kuò)大生產(chǎn),使今后兩年的產(chǎn)值都比前一年增長一個(gè)相同的百分?jǐn)?shù)����,這樣三年(包括今年)的總產(chǎn)值就達(dá)到了1400萬元.設(shè)這個(gè)百分?jǐn)?shù)為x����,則可列方程為( )
A.
B.
C.
D.
10����、在小孔成像問題中,根據(jù)如圖所示��,若O到AB的距離是18 cm�����,O到CD的距離是6 cm�����, 則像CD的長是物體AB長的 ( )
A.3倍 B. C. D.2
4�、倍
11�、如圖,A�����、B兩點(diǎn)在雙曲線y=上,分別經(jīng)過A�、B兩點(diǎn)向坐標(biāo)軸作垂線段,已知S陰影=1�,則S1+S2=( )
A.3 B.4 C.5 D.6
12�、如圖,已知四邊形OABC為正方形�,邊長為6,點(diǎn)A���、C分別在x軸�����、y軸的正半軸上���,點(diǎn)D在OA上,且點(diǎn)D的坐標(biāo)為(2����,0),點(diǎn)P是OB上的一個(gè)動(dòng)點(diǎn)���,則PD+PA的最小值是( )
A.6 B.8 C. D.
二��、選擇題(每小題3分�����,共12分)
13��、若x1=-1是關(guān)于x的方程x2+m
5�����、x-5=0的一個(gè)根��,則此方程的另一個(gè)根x2= .
14���、如圖�����,小明從路燈下,向前走了5米����,發(fā)現(xiàn)自己在地面上的影子長DE是2米. 如果小明的身高 為1.6米,那么路燈高地面的高度AB是 米.
15�����、如圖17,正方形的邊長為�,分別交于點(diǎn),在上任取兩點(diǎn)��,那么圖中陰影部分的面積是 .
16����、如圖所示,已知菱形OABC�����,點(diǎn)C在x軸上�,直線y=x經(jīng)過點(diǎn)A,菱形OABC的面積是.若反比例函數(shù)y=的圖象經(jīng)過點(diǎn)B���,則此反比例函數(shù)表達(dá)式中的K為 .
三�����、解答題(共52分)
17���、用適當(dāng)
6�����、的方法解下列方程(每小題4分�,共8分)
(1) ?����。?)
18�、在一個(gè)不透明的箱子里,裝有紅���、白���、黑各一個(gè)球,它們除了顏色之外沒有其他區(qū)別.
(1)隨機(jī)地從箱子里取出1個(gè)球��,則取出紅球的概率是多少��?(2分)
(2)隨機(jī)地從箱子里取出1個(gè)球�����,放回?cái)噭蛟偃〉诙€(gè)球�����,請你用畫樹狀圖或列表的方法表示所有等可能的結(jié)果��,并求兩次取出相同顏色球的概率.(4分)
A
B
C
P
Q
M
N
19�、(6分)在同一時(shí)刻兩根木竿在太陽光下的影子如圖所示,其中木竿AB=2米��,它的影子BC=1.6米�����,木竿PQ的影子有一部分落在墻上��,PM=1.2米�����,
7�、MN=0.8米,求木竿PQ的長度�。
20、如圖�,在△ABC中,AD是BC邊上的中線���,E是AD的中點(diǎn)�,過點(diǎn)A作BC的平行線交BE的延長線于點(diǎn)F,連接CF.
(1)求證:AF=DC����;(3分)
(2)若AB⊥AC,試判斷四邊形ADCF的形狀����,并證明你的結(jié)論.(4分)
21、(8分)某超市經(jīng)銷一種成本為40元/的水產(chǎn)品���,市場調(diào)查發(fā)現(xiàn)�����,按50元/銷售�,一個(gè)月能售出500���,銷售單價(jià)每漲1元�����,月銷售量就減少10�,針對(duì)這種水產(chǎn)品的銷售情況,超市在月成本不超過10000元的情況下����,使得月銷售利潤達(dá)到8000元�����,請你幫忙算算���,銷售
8�、單價(jià)定為多少���?
22����、如圖��,四邊形ABCD為正方形.點(diǎn)A的坐標(biāo)為(0�����,2),點(diǎn)B的坐標(biāo)為(0��,-3)����,反比例函數(shù)y=的圖象經(jīng)過點(diǎn)C,一次函數(shù)y=ax+b的圖象經(jīng)過點(diǎn)A ���,C����。
(1)求反比例函數(shù)與一次函數(shù)的解析式(4分)���;
(2)若點(diǎn)P是反比例函數(shù)圖象上的一點(diǎn)����,△OAP的面積恰好等于正方形ABCD的面積�����,求P點(diǎn)的坐標(biāo)(4分).
23�、已知矩形ABCD的一條邊AD=8,將矩形ABCD折疊��,使得頂點(diǎn)B落在CD邊上的P點(diǎn)處.
(1)如圖,已知折痕與邊BC交于點(diǎn)E�����,連結(jié)AP�、EP、EA.
求證:△ECP∽△PDA����;(3分)
(2)若△ECP與△PDA的面積比為1:4�����,
9�����、求邊AB的長�����;(3分)
(3)在(2)的條件下以點(diǎn)A為坐標(biāo)原點(diǎn)��,AB所在直線為x軸�,
AD所在直線為y軸建立平面直角坐標(biāo)系,問在坐標(biāo)平面內(nèi)是否存 在點(diǎn)M,使得以點(diǎn)A�、B、E�����、M為頂點(diǎn)的四邊形是平行四邊形�,若存在請
直接寫出點(diǎn)M的坐標(biāo);若不存在請說明理由��。(3分)
九年級(jí)數(shù)學(xué)(上)期中測試題答題卡
班級(jí) 姓名 得分
一��、選擇題(每小題3分��,共36分)
1
2
10�、
3
4
5
6
7
8
9
10
11
12
A
B
A
B
C
B
C
B
D
C
D
D
二、填空題 (本題滿分12分)
13. 5 �; 14. 5.6 ; 15. 8 �����; 16. +1 ����;
三�����、解答題(共52分)
17.用適當(dāng)?shù)姆椒ń庀铝蟹匠蹋啃☆}4分�,共8分)
18.(1)(2
11��、分)解:P(取出紅球)=
(2)(4分)解:列表如下:
紅
白
黑
紅
(紅��,紅)
(白���,紅)
(黑�,紅)
白
(紅��,白)
(白�����,白)
(黑��,白)
黑
(紅�,黑)
(白����,黑)
(黑�,黑)
由上表可知共有9種等可能的結(jié)果���,其中P(兩次取出相同顏色球)=
19.(6分)解:
如圖過點(diǎn)N作PQ的垂線段�����,垂足為D����,則有
DN=PM=1.2米���,DP=MN=0.8米����。由題意有: D
20.
(
12��、1)(4分)解:
證明:∵AF∥BC��,
∴∠AFE=∠DBE����,
∵E是AD的中點(diǎn),AD是BC邊上的中線���,
∴AE=DE���,BD=CD�,
在△AFE和△DBE中:
∴△AFE≌△DBE(AAS)���,
∴AF=BD��,
∴AF=DC.
(2)(4分)解:四邊形ADCF是菱形��,
證明:AF∥BC�����,AF=DC���,
∴四邊形ADCF是平行四邊形����,
∵AC⊥AB,AD是斜邊BC的中線�����,
∴AD=BC=DC,
∴平行四邊形ADCF是菱形.
21.(8分)解:設(shè)銷售單價(jià)為x元/kg�,由題意有
(x–40)[500–(x–50)×10]=8000
解
13、得: x1=60 x2=80
當(dāng)x=60時(shí)代入500–(x–50)×10中得500–(60–50)×10=400
40×400=16000元>10000舍去
當(dāng)x=80時(shí)代入500–(x–50)×10中得500–(80–50)×10=200
40×200=8000元<10000符合
∴當(dāng)銷售單價(jià)應(yīng)定為80元/kg�����。
22.(1)(4分)解::(1)∵點(diǎn)A的坐標(biāo)為(0���,2)����,點(diǎn)B的坐標(biāo)為(0�,﹣3),
∴AB=5���,
∵四邊形ABCD為正方形�,
∴點(diǎn)C的坐標(biāo)為(5��,﹣3).
∵反比例函數(shù)y=的圖象經(jīng)過點(diǎn)C��,
∴﹣3=���,
14����、解得k=﹣15,
∴反比例函數(shù)的解析式為y=﹣�����;
∵一次函數(shù)y=ax+b的圖象經(jīng)過點(diǎn)A�����,C��,
∴�����, 解得���,
∴一次函數(shù)的解析式為y=﹣x+2�;
(2)(4分)解:設(shè)P點(diǎn)的坐標(biāo)為(x��,y). ∵△OAP的面積恰好等于正方形ABCD的面積��,
∴×OA?|x|=52���,
∴×2?|x|=25��, 解得x=±25.
當(dāng)x=25時(shí)��,y=﹣=﹣���; 當(dāng)x=﹣25時(shí),y=﹣=.
∴P點(diǎn)的坐標(biāo)為(25����,﹣)或(﹣25,).
23.
(1)(3分)解:
∵四邊形ABCD是矩形���,∴AD=BC�����,DC=AB�,
15�����、∠DAB=∠B=∠C=∠D=90°.
由折疊可得:AP=AB,PE=BE�,∠PAE=∠BAE.∠APE=∠B.
∴∠APE=90°.
∴∠APD=90°﹣∠CPE=∠PEC.
∵∠D=∠C,∠APD=∠PEC.
∴△ECP∽△PDA.
(2)(3分)解:∵△ECP與△PDA的面積比為1:4���,
∴ = = == .
∴PD=2EC���,PA=2EP,DA=2CP.
∵AD=8����,∴CP=4,BC=8.
設(shè)EP=x��,則EB=x���,CE=8﹣x.
在Rt△PCE中�����,
∵∠C=90°�,CP=4���,EP=x�����,CE=8﹣x��,
∴x2=(8﹣x)2+42.
解得:x=5.
∴AB=AP=2EP=10.
∴邊AB的長為10.
23.(3)(3分)解:
M1(20,5)
M2(0,5)
M3(0,-5)
 九年級(jí)數(shù)學(xué)上學(xué)期期中試題 北師大版(I)
九年級(jí)數(shù)學(xué)上學(xué)期期中試題 北師大版(I)