《蘇教版數(shù)學(xué)選修2-1:第2章 圓錐曲線與方程 第2章章末總結(jié) 課時作業(yè)(含答案)》由會員分享�,可在線閱讀���,更多相關(guān)《蘇教版數(shù)學(xué)選修2-1:第2章 圓錐曲線與方程 第2章章末總結(jié) 課時作業(yè)(含答案)(8頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1���、
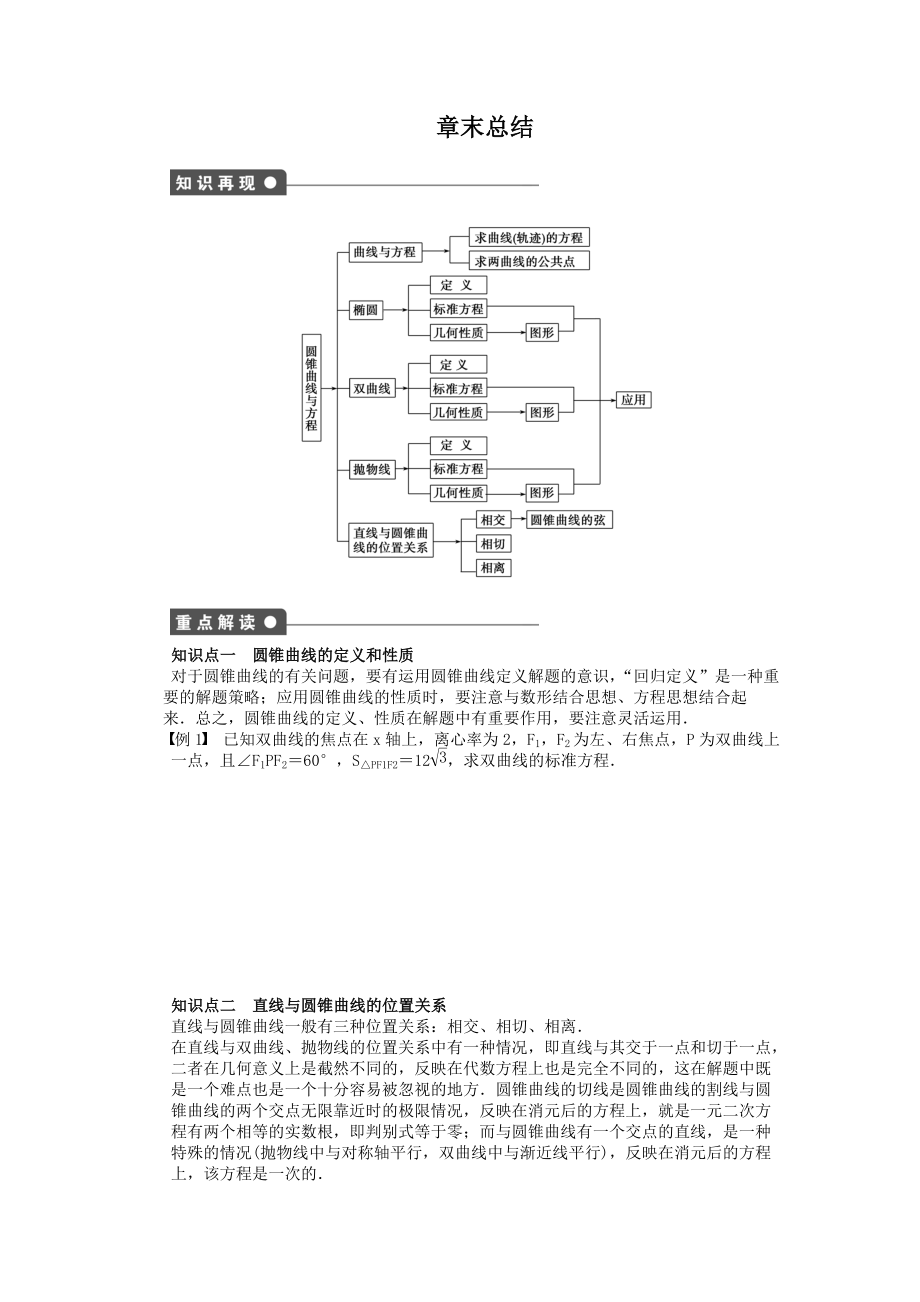
章末總結(jié)
知識點(diǎn)一 圓錐曲線的定義和性質(zhì)
對于圓錐曲線的有關(guān)問題����,要有運(yùn)用圓錐曲線定義解題的意識�,“回歸定義”是一種重要的解題策略;應(yīng)用圓錐曲線的性質(zhì)時����,要注意與數(shù)形結(jié)合思想、方程思想結(jié)合起來.總之����,圓錐曲線的定義、性質(zhì)在解題中有重要作用�,要注意靈活運(yùn)用.
例1 已知雙曲線的焦點(diǎn)在x軸上,離心率為2�����,F(xiàn)1,F(xiàn)2為左�、右焦點(diǎn),P為雙曲線上一點(diǎn)����,且∠F1PF2=60,S△PF1F2=12��,求雙曲線的標(biāo)準(zhǔn)方程.
知識點(diǎn)二 直線與圓錐曲線的位置關(guān)系
直線與圓錐曲線一般有三種位置關(guān)系:相交���、相切���、相離.
在直線與
2、雙曲線���、拋物線的位置關(guān)系中有一種情況�,即直線與其交于一點(diǎn)和切于一點(diǎn)��,二者在幾何意義上是截然不同的����,反映在代數(shù)方程上也是完全不同的��,這在解題中既是一個難點(diǎn)也是一個十分容易被忽視的地方.圓錐曲線的切線是圓錐曲線的割線與圓錐曲線的兩個交點(diǎn)無限靠近時的極限情況���,反映在消元后的方程上,就是一元二次方程有兩個相等的實(shí)數(shù)根����,即判別式等于零��;而與圓錐曲線有一個交點(diǎn)的直線����,是一種特殊的情況(拋物線中與對稱軸平行,雙曲線中與漸近線平行)�,反映在消元后的方程上,該方程是一次的.
例2
如圖所示�,O為坐標(biāo)原點(diǎn),過點(diǎn)P(2�,0)且斜率為k的直線l交拋物線y2=2x于M(x1,y1)��,N(x2�,y2)兩
3、點(diǎn).
(1)求x1x2與y1y2的值���;
(2)求證:OM⊥ON.
知識點(diǎn)三 軌跡問題
軌跡是解析幾何的基本問題�����,求解的方法有以下幾種:
(1)直接法:建立適當(dāng)?shù)淖鴺?biāo)系�����,設(shè)動點(diǎn)為(x����,y),根據(jù)幾何條件直接尋求x����、y之間的關(guān)系式.
(2)代入法:利用所求曲線上的動點(diǎn)與某一已知曲線上的動點(diǎn)的關(guān)系,把所求動點(diǎn)轉(zhuǎn)換為已知動點(diǎn).具體地說���,就是用所求動點(diǎn)的坐標(biāo)x���、y來表示已知動點(diǎn)的坐標(biāo)并代入已知動點(diǎn)滿足的曲線的方程,由此即可求得所求動點(diǎn)坐標(biāo)x����、y之間的關(guān)系式.
(3)定義法:如果所給幾何條件正好符合圓���、橢圓、雙曲線���、拋物線等曲線的定義���,則
4、可直接利用這些已知曲線的方程寫出動點(diǎn)的軌跡方程.
(4)參數(shù)法:當(dāng)很難找到形成曲線的動點(diǎn)P(x�,y)的坐標(biāo)x����,y所滿足的關(guān)系式時,借助第三個變量t����,建立t和x,t和y的關(guān)系式x=φ(t)���,y=Φ(t)���,再通過一些條件消掉t就間接地找到了x和y所滿足的方程,從而求出動點(diǎn)P(x,y)所形成的曲線的普通方程.
例3 設(shè)點(diǎn)A�、B是拋物線y2=4px (p>0)上除原點(diǎn)O以外的兩個動點(diǎn),已知OA⊥OB���,OM⊥AB����,垂足為M�����,求點(diǎn)M的軌跡方程���,并說明它表示什么曲線����?
知識點(diǎn)四 圓錐曲線中的定點(diǎn)�����、定值問題
圓錐曲線中的定點(diǎn)�����、定值問題是高考命題的一個熱點(diǎn)
5、��,也是圓錐曲線問題中的一個難點(diǎn)����,解決這個難點(diǎn)沒有常規(guī)的方法,但解決這個難點(diǎn)的基本思想是明確的�,定點(diǎn)、定值問題必然是在變化中所表現(xiàn)出來的不變的量�,那么就可以用變化的量表示問題的直線方程
、數(shù)量積�、比例關(guān)系等,這些直線方程��、數(shù)量積��、比例關(guān)系不受變化的量所影響的某個點(diǎn)或值�,就是要求的定點(diǎn)�、定值.化解這類問題難點(diǎn)的關(guān)鍵就是引進(jìn)變化的參數(shù)表示直線方程、數(shù)量積�、比例關(guān)系等,根據(jù)等式的恒成立�、數(shù)式變換等尋找不受參數(shù)影響的量.
例4 若直線l:y=kx+m與橢圓+=1相交于A、B兩點(diǎn)(A�、B不是左、右頂點(diǎn)),A2為橢圓的右頂點(diǎn)且AA2⊥BA2���,求證:直線l過定點(diǎn).
6、
知識點(diǎn)五 圓錐曲線中的最值���、范圍問題
圓錐曲線中的最值���、范圍問題�,是高考熱點(diǎn)�,主要有以下兩種求解策略:
(1)平面幾何法
平面幾何法求最值問題�����,主要是運(yùn)用圓錐曲線的定義和平面幾何知識求解.
(2)目標(biāo)函數(shù)法
建立目標(biāo)函數(shù)解與圓錐曲線有關(guān)的最值問題��,是常規(guī)方法��,其關(guān)鍵是選取適當(dāng)?shù)淖兞拷⒛繕?biāo)函數(shù),然后運(yùn)用求函數(shù)最值的方法確定最值.
例5 已知A(4,0)����,B(2,2)是橢圓+=1內(nèi)的兩定點(diǎn),點(diǎn)M是橢圓上的動點(diǎn)��,求MA+MB的最值.
例6 已知F1�����、F2為橢圓x2+=1的上、下兩個焦點(diǎn)�����,AB是過焦點(diǎn)
7�����、F1的一條動弦����,求△ABF2面積的最大值.
章末總結(jié)
重點(diǎn)解讀
例1 解
如圖所示,設(shè)雙曲線方程為-=1 (a>0��,b>0).
∵e==2����,∴c=2a.
由雙曲線的定義�,
得|PF1-PF2|=2a=c��,
在△PF1F2中,由余弦定理�,得:
F1F=PF+PF-2PF1PF2cos 60
=(PF1-PF2)2+2PF1PF2(1-cos 60)�,
即4c2=c2+PF1PF2.①
又S△PF1F2=12�����,
∴PF1PF2sin 60=12�����,
即PF1PF2=48.②
由①②,得c2=16�,c=4��,則a=2�,b2=c2-a2=
8�、12�,
∴所求的雙曲線方程為-=1.
例2 (1)解 過點(diǎn)P(2,0)且斜率為k的直線方程為:y=k(x-2).
把y=k(x-2)代入y2=2x�����,
消去y得k2x2-(4k2+2)x+4k2=0,
由于直線與拋物線交于不同兩點(diǎn)��,
故k2≠0且Δ=(4k2+2)2-16k4=16k2+4>0�����,
x1x2=4��,x1+x2=4+�,
∵M(jìn)、N兩點(diǎn)在拋物線上�,
∴yy=4x1x2=16����,
而y1y2<0����,∴y1y2=-4.
(2)證明∵ =(x1���,y1), =(x2�����,y2)���,
∴=x1x2+y1y2=4-4=0.
∴⊥�����,即OM⊥ON.
例3 解 設(shè)直線OA的方程為y=kx
9����、 (k≠1���,因?yàn)楫?dāng)k=1時,直線AB的斜率不存在)���,則直線OB的方程為y=-,進(jìn)而可求A�����、
B(4pk2,-4pk).
于是直線AB的斜率為kAB=�,
從而kOM=����,
∴直線OM的方程為y=x,①
直線AB的方程為y+4pk=(x-4pk2).②
將①②相乘��,得y2+4pky=-x(x-4pk2),
即x2+y2=-4pky+4pk2x=4p(k2x-ky)�����,③
又k2x-ky=x,代入③式并化簡�����,
得(x-2p)2+y2=4p2.
當(dāng)k=1時,易求得直線AB的方程為x=4p.
故此時點(diǎn)M的坐標(biāo)為(4p,0)����,也在(x-2p)2+y2=4p2 (x≠0)上.
∴
10�、點(diǎn)M的軌跡方程為(x-2p)2+y2=4p2 (x≠0),
∴其軌跡是以(2p,0)為圓心��,半徑為2p的圓�,去掉坐標(biāo)原點(diǎn).
例4
證明 設(shè)A(x1,y1)�����,
B(x2�,y2),
聯(lián)立
得(3+4k2)x2+8mkx+4(m2-3)=0����,
則
即
又y1y2=(kx1+m)(kx2+m)
=k2x1x2+mk(x1+x2)+m2
=.
∵橢圓的右頂點(diǎn)為A2(2,0),AA2⊥BA2�����,
∴(x1-2)(x2-2)+y1y2=0.
∴y1y2+x1x2-2(x1+x2)+4=0.
∴+++4=0.
∴7m2+16km+4k2=0���,
解得m1=-2k����,m2=-�,
11、且均滿足3+4k2-m2>0.
當(dāng)m1=-2k時���,l的方程為y=k(x-2)�,
直線過定點(diǎn)(2,0),與已知矛盾.
當(dāng)m2=-時�,l的方程為y=k,直線過定點(diǎn)��,∴直線l過定點(diǎn).
例5 解 因?yàn)锳(4,0)是橢圓的右焦點(diǎn)�����,設(shè)A′為橢圓的左
焦點(diǎn)�����,則A′(-4,0)�,由橢圓定義知MA+MA′=10.
如圖所示��,則MA+MB=MA+MA′+MB-MA′=10+MB-MA′≤10+A′B.
當(dāng)點(diǎn)M在BA′的延長線上時取等號.
所以當(dāng)M為射線BA′與橢圓的交點(diǎn)時����,
(MA+MB)max=10+A′B=10+2.
又如圖所示,MA+MB=MA+MA′-MA′+MB
=10-(MA′-MB)
≥10-A′B�,
當(dāng)M在A′B的延長線上時取等號.
所以當(dāng)M為射線A′B與橢圓的交點(diǎn)時,
(MA+MB)min=10-A′B=10-2.
例6 解 由題意����,F(xiàn)1F2=2.
設(shè)直線AB方程為y=kx+1����,
代入橢圓方程2x2+y2=2��,
得(k2+2)x2+2kx-1=0����,
則xA+xB=-,xAxB=-�,
∴|xA-xB|=.
S△ABF2=F1F2|xA-xB|=2
=2≤2=.
當(dāng)=,即k=0時���,
S△ABF2有最大面積為.
希望對大家有所幫助���,多謝您的瀏覽!
 蘇教版數(shù)學(xué)選修2-1:第2章 圓錐曲線與方程 第2章章末總結(jié) 課時作業(yè)(含答案)
蘇教版數(shù)學(xué)選修2-1:第2章 圓錐曲線與方程 第2章章末總結(jié) 課時作業(yè)(含答案)