《九年級(jí)數(shù)學(xué)上冊(cè)第23章圖形的相似第8課時(shí)相似三角形的性質(zhì)導(dǎo)學(xué)案新華東師大版》由會(huì)員分享，可在線閱讀，更多相關(guān)《九年級(jí)數(shù)學(xué)上冊(cè)第23章圖形的相似第8課時(shí)相似三角形的性質(zhì)導(dǎo)學(xué)案新華東師大版（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、▼▼▼2019屆華師大版數(shù)學(xué)資料▼▼▼
相似三角形的性質(zhì)
課 題
課型
學(xué)生姓名
組別
學(xué)生評(píng)價(jià)
教師評(píng)價(jià)
相似三角形的性質(zhì)
新授課
一、學(xué)習(xí)目標(biāo)
經(jīng)歷探索相似三角形性質(zhì)的過程，能運(yùn)用性質(zhì)進(jìn)行有關(guān)的計(jì)算。
二、學(xué)習(xí)重點(diǎn)
利用相似三角形的性質(zhì)解決計(jì)算問題。
三、自主預(yù)習(xí)
1．識(shí)別兩個(gè)三角形相似的簡(jiǎn)便（判定）方法有哪些？
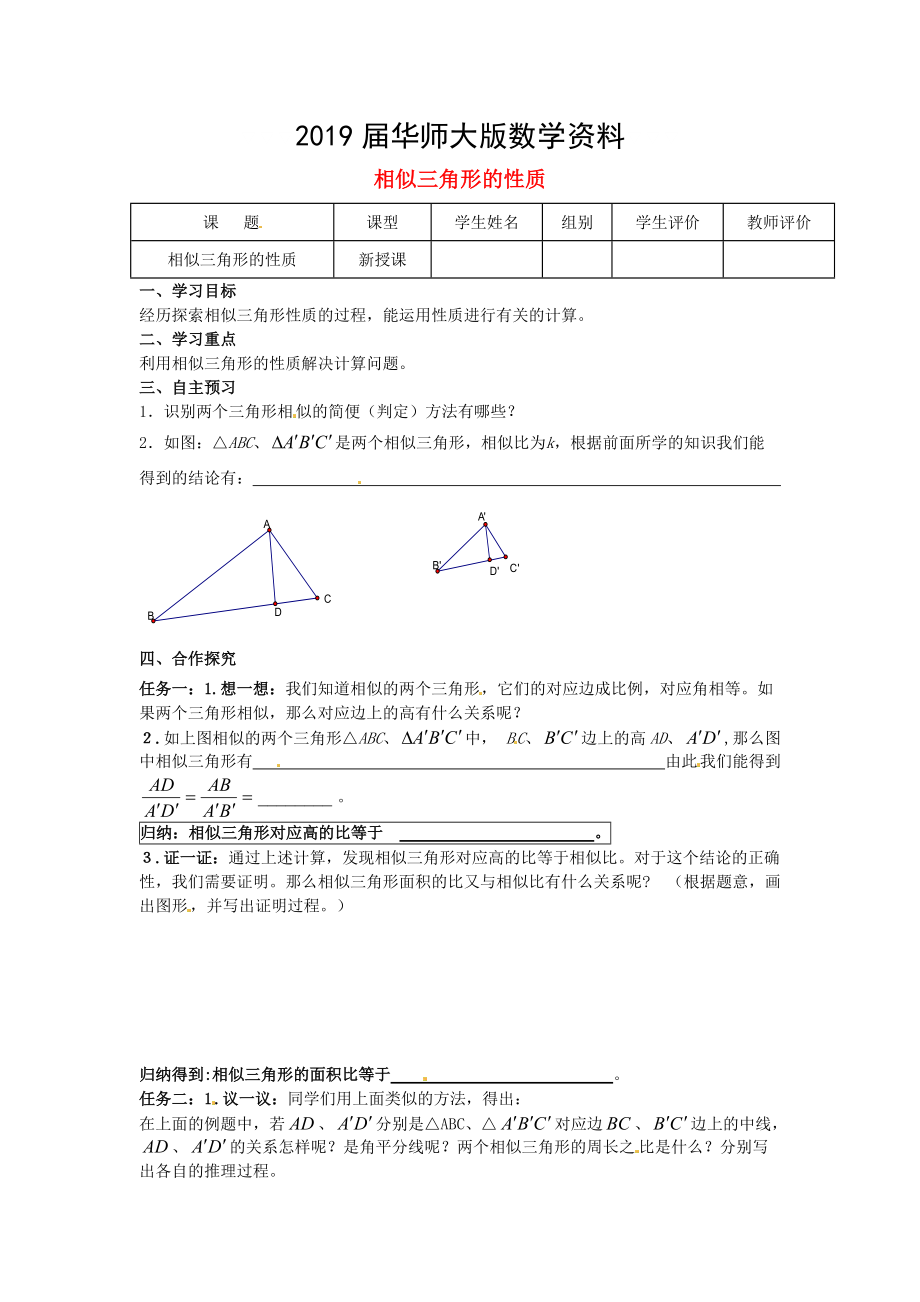
2．如圖：△ABC、是兩個(gè)相似三角形，相似比為k，根據(jù)前面所學(xué)的知識(shí)我們能得到的結(jié)論有：
2、
四、合作探究
任務(wù)一：1.想一想：我們知道相似的兩個(gè)三角形，它們的對(duì)應(yīng)邊成比例，對(duì)應(yīng)角相等。如果兩個(gè)三角形相似，那么對(duì)應(yīng)邊上的高有什么關(guān)系呢？
２.如上圖相似的兩個(gè)三角形△ABC、中， BC、邊上的高AD、,那么圖中相似三角形有 由此我們能得到。
歸納：相似三角形對(duì)應(yīng)高的比等于 。
３.證一證：通過上述計(jì)算，發(fā)現(xiàn)相似三角形對(duì)應(yīng)高的比等于相似比。對(duì)于這個(gè)結(jié)論的正確性，我們需要證明。那么相似三角形面積的比又與相似比有什么關(guān)系呢? （根據(jù)題意，畫出圖形，并
3、寫出證明過程。）
歸納得到:相似三角形的面積比等于 。
任務(wù)二：1.議一議：同學(xué)們用上面類似的方法，得出：
在上面的例題中，若、分別是△ABC、△對(duì)應(yīng)邊、邊上的中線，、的關(guān)系怎樣呢？是角平分線呢？?jī)蓚€(gè)相似三角形的周長(zhǎng)之比是什么？分別寫出各自的推理過程。
歸納得到:相似三角形的對(duì)應(yīng)角平分線之比等于 。
相似三角形的中線之比等于 。
相似三角形的周長(zhǎng)之比等于
4、 。
五、鞏固反饋（當(dāng)堂檢測(cè)）
★【基礎(chǔ)知識(shí)練習(xí)】
1．教材課后練習(xí)題。
★【提高拓展練習(xí)】
1.如左下圖：D是△ABC的邊AB上一點(diǎn)，過D作DE∥BC交AC于E，已知AD：BD=3：2， 。
2.已知：如右上圖，在△ABC中，AD是高，矩形EFGH內(nèi)接于△ABC，且長(zhǎng)邊FG在BC上，矩形相鄰兩邊的比為1：2，若BC=30㎝,AD=10㎝,求矩形EFGH的面積。
★【中考考點(diǎn)鏈接】
1.(2013年聊城)如圖，D是△ABC的邊BC上一點(diǎn)，已知AB=4，AD=2．∠DAC=∠B，若△ABD的面積為a，則△ACD的面積為（ ?。?
精品華師大版教學(xué)資料
精品華師大版教學(xué)資料
九年級(jí)數(shù)學(xué)上冊(cè)第23章圖形的相似第8課時(shí)相似三角形的性質(zhì)導(dǎo)學(xué)案新華東師大版
