《2018-2019學(xué)年九年級(jí)數(shù)學(xué)上《第24章圓》單元檢測(cè)試題》由會(huì)員分享���,可在線閱讀���,更多相關(guān)《2018-2019學(xué)年九年級(jí)數(shù)學(xué)上《第24章圓》單元檢測(cè)試題(12頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
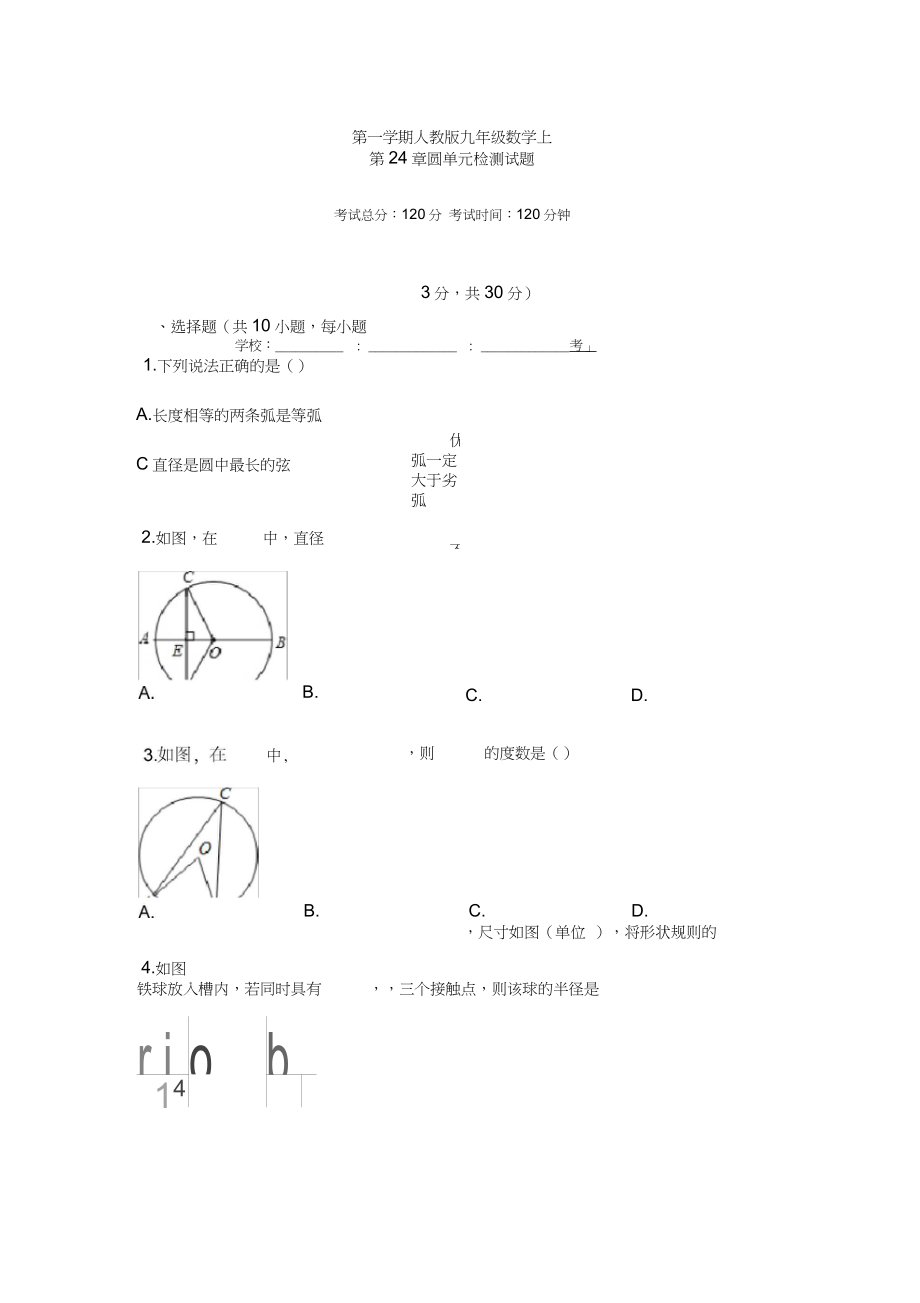
1�����、第一學(xué)期人教版九年級(jí)數(shù)學(xué)上第24章圓單元檢測(cè)試題考試總分:120分 考試時(shí)間:120分鐘學(xué)校:_: _ : _考鐵球放入槽內(nèi)�����,若同時(shí)具有���,三個(gè)接觸點(diǎn)���,則該球的半徑是r.i ob14�、選擇題(共10小題���,每小題3分�����,共30分)1.下列說法正確的是()A.長度相等的兩條弧是等弧C直徑是圓中最長的弦2.如圖�����,在中����,直徑優(yōu)弧一定大于劣弧不C.D.����,則的度數(shù)是()B.C.D.4.如圖所示的�,尺寸如圖(單位 ),將形狀規(guī)則的B.中,A.B.C.D.C若是F列判斷正確的是的中點(diǎn)���,貝U定是此圓的圓心D.是圓的直徑�,弦當(dāng)B為圓心時(shí),相交于點(diǎn)���,是的中6.如圖,C.DL7.的半徑為的一條弦長����,以為半徑的同心圓與直線
2、的位置關(guān)系是(A相離B.相交C相切D.不能確定的外接圓���,已知���,則的大小為()B.C.D.9.正方形的外接圓半徑與內(nèi)切圓的半徑之比為(A.B.C.D.10.已知一個(gè)圓錐形的漏斗側(cè)面展開圖的圓心角為圓錐的高為則圓錐的全面積()A.B.C.D.,則 大小為_,分別以����,為圓心,、填空題(共10小題��,每小題3分����,共30分)_ .(結(jié)果用含的式子表示)16.已知圓錐的母線長為,側(cè)面展開后所得扇形的圓心角為��,貝U該圓錐的底面半徑為_ _17.如圖�,圓柱底面半徑為,高為 �����,點(diǎn)、分別是圓柱兩底面圓周上的點(diǎn)��,且�����、 在同一母線上��,用一棉線從 順著圓柱側(cè)面繞 圈到���,求棉線最11.已知的面積為�����,當(dāng)時(shí)�,點(diǎn)在上.12.在中
3�、,的圓心角所對(duì)的弧長是,則的半徑13.已知����,點(diǎn)在的平分線上,�����,以為圓心,為半徑作圓,則與的位置關(guān)系是14.現(xiàn)有一個(gè)邊長為的正方形�,繞它的一邊旋轉(zhuǎn)一周,得到的幾何體體積是15.個(gè)圓錐的側(cè)面積是,底面直徑是���,則這個(gè)圓錐的母線長是中,以 為半徑畫弧�����,三條弧與所圍成的陰影部分的周長是20.已知等腰內(nèi)接于�,底邊 ����,圓心到則腰長 _.三、解答題(共6小題�����,每小題10分�,共60分)21.如圖.是半圓的直徑,為中點(diǎn)��,、兩點(diǎn)在弧連接 ����、.若的度數(shù)為,求ft的度數(shù).上���,且的一條弦����,點(diǎn)是弧的中點(diǎn),于點(diǎn)�,點(diǎn)在22.如圖,是����,求的度數(shù).23.如圖,已知 是 的弦,是弦上任意一點(diǎn)(不的距離等于以 為半徑畫弧����,三條弧與所圍
4、成的陰影部分的周長是與點(diǎn)�����、重合),連接并延長弦 _ 吉果保留根號(hào));當(dāng)時(shí)�,求的度數(shù).是 的直徑,求證:,在運(yùn)動(dòng)過程中,點(diǎn)、始終在直線 上��,設(shè)運(yùn)動(dòng)時(shí)間為�����,當(dāng)時(shí)�,半圓在 的左側(cè)����,當(dāng)時(shí),點(diǎn)在半圓_當(dāng)時(shí)���,點(diǎn)在半圓_ _當(dāng)為何值時(shí)�����,的邊與半圓相切��?當(dāng)為何值時(shí)�,的邊與半圓相切����?26.如圖,有一直徑的半圓形紙片,其圓心為點(diǎn)��,從初始位置 開始�����,在無滑動(dòng)的情況下沿?cái)?shù)軸向右翻滾至位置����,其中,位置 中的平行于數(shù)軸,且半與數(shù)軸相切于原點(diǎn) ����;位置和位置 中的 垂直于數(shù)軸;位置 中的 在數(shù)軸上��;位置 中半與數(shù)軸相切于點(diǎn)�,且此時(shí)為等邊三角 形.25.如圖,形如量角器的半圓的直徑,形如三角板的中,14.解答下列問題:(各小問結(jié)果保留)位置 中的點(diǎn) 到直線 的距離為_位置 中的半位置中的圓心在數(shù)軸上表示的數(shù)為_求的長.答案1. C2. B3. D4. A5. B6. A7. C8. A9. A10. B11.12.13.相交位置關(guān)系是_ _與數(shù)軸的15.16.17.18.19.-20.或 _21.解:是直徑,的度數(shù)是:22.解:點(diǎn)是弧的中點(diǎn),23解:如圖�,過作于,I是 的中點(diǎn)���,中,又解法二:如圖�����,連接又. ?(同弧所對(duì)的圓周角等于它所對(duì)圓心角的一半)24.解:于,是的直徑,的中點(diǎn)��,的中位線,中����,即為等邊三角形����,從而弧 的長為,于是 的長為點(diǎn)是是在25.外外26.相切
 2018-2019學(xué)年九年級(jí)數(shù)學(xué)上《第24章圓》單元檢測(cè)試題
2018-2019學(xué)年九年級(jí)數(shù)學(xué)上《第24章圓》單元檢測(cè)試題