《山東省高中數(shù)學(xué)新課標(biāo)人教A版必修三第3章 概率導(dǎo)學(xué)案》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《山東省高中數(shù)學(xué)新課標(biāo)人教A版必修三第3章 概率導(dǎo)學(xué)案（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
第三章復(fù)習(xí)
授課
時(shí)間
第 周 星期 第 節(jié)
課型
復(fù)習(xí)課
主備課人
學(xué)習(xí)
目標(biāo)
1．掌握概率的基本性質(zhì)
2．學(xué)會(huì)古典概型和幾何概型簡(jiǎn)單運(yùn)用
重點(diǎn)難點(diǎn)
重點(diǎn) 古典概型、幾何概型的相關(guān)知識(shí)點(diǎn)
難點(diǎn) 古典概型、幾何概型的具體應(yīng)用
學(xué)習(xí)
過(guò)程
與方
法
自主學(xué)習(xí)
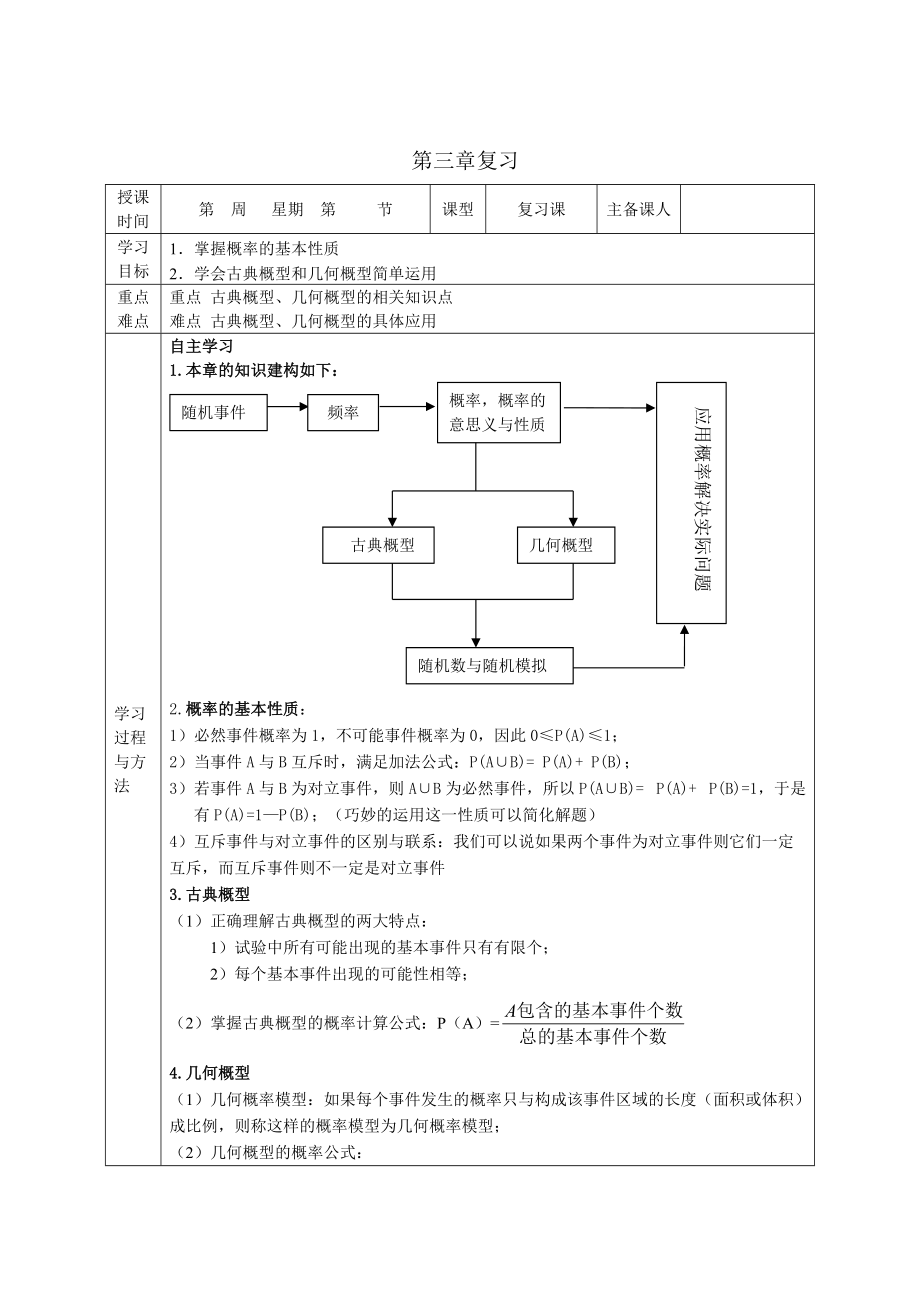
1.本章的知識(shí)建構(gòu)如下：
隨機(jī)事件
頻率
概率，概率的意思義與性質(zhì)
應(yīng)用概率解決實(shí)際問(wèn)題
古典概型
幾何概型
隨機(jī)數(shù)與隨機(jī)模擬
2.概率的基本性質(zhì)：
1）必然事件概率為1，不可能事件概率為0，因此0≤P(A)≤1；
2）當(dāng)事件A
2、與B互斥時(shí)，滿(mǎn)足加法公式：P(A∪B)= P(A)+ P(B)；
3）若事件A與B為對(duì)立事件，則A∪B為必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)；（巧妙的運(yùn)用這一性質(zhì)可以簡(jiǎn)化解題）
4）互斥事件與對(duì)立事件的區(qū)別與聯(lián)系：我們可以說(shuō)如果兩個(gè)事件為對(duì)立事件則它們一定互斥，而互斥事件則不一定是對(duì)立事件
3.古典概型
（1）正確理解古典概型的兩大特點(diǎn)：
1）試驗(yàn)中所有可能出現(xiàn)的基本事件只有有限個(gè)；
2）每個(gè)基本事件出現(xiàn)的可能性相等；
（2）掌握古典概型的概率計(jì)算公式：P（A）=
4.幾何概型
（1）幾何概率模型：如果每個(gè)事件發(fā)生的概率只與構(gòu)
3、成該事件區(qū)域的長(zhǎng)度（面積或體積）成比例，則稱(chēng)這樣的概率模型為幾何概率模型；
（2）幾何概型的概率公式：
P（A）=；
（3）幾何概型的特點(diǎn)：1）試驗(yàn)中所有可能出現(xiàn)的結(jié)果（基本事件）有無(wú)限多個(gè)；
2）每個(gè)基本事件出現(xiàn)的可能性相等．
5.古典概型和幾何概型的區(qū)別 相同：兩者基本事件的發(fā)生都是等可能的；
不同：古典概型要求基本事件有有限個(gè)，
幾何概型要求基本事件有無(wú)限多個(gè).
精講互動(dòng)
例1、柜子里裝有3雙不同的鞋，隨機(jī)地取出2只，試求下列事件的概率
（1）取出的鞋子都是左腳的;
（2）取出的鞋子都是同一只腳的
（選作）變式：（1）取出的鞋一只是左腳的，一只是右腳的；
（2）取出的鞋不成對(duì)
例2、取一根長(zhǎng)為3 m的繩子，拉直后在任意位置剪斷，那么剪得兩段的長(zhǎng)度都不小于1m的概率有多大？
達(dá)標(biāo)訓(xùn)練
1. 課本p161 復(fù)習(xí)題三 A組：1 2 3 4 5 6
2. 教輔資料
作業(yè)
布置
1.復(fù)習(xí)題三 A組：7 、8、 9、 10 、11
2.教輔資料
學(xué)習(xí)小結(jié)/教學(xué)
反思
最新精品語(yǔ)文資料
山東省高中數(shù)學(xué)新課標(biāo)人教A版必修三第3章 概率導(dǎo)學(xué)案
