《人教版八年級上冊數(shù)學(xué) 12.2全等三角形的判定（SAS）同步練習(xí)（無答案）》由會員分享，可在線閱讀，更多相關(guān)《人教版八年級上冊數(shù)學(xué) 12.2全等三角形的判定（SAS）同步練習(xí)（無答案）（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、全等三角形的判定二（SAS）作業(yè)
一、填空題
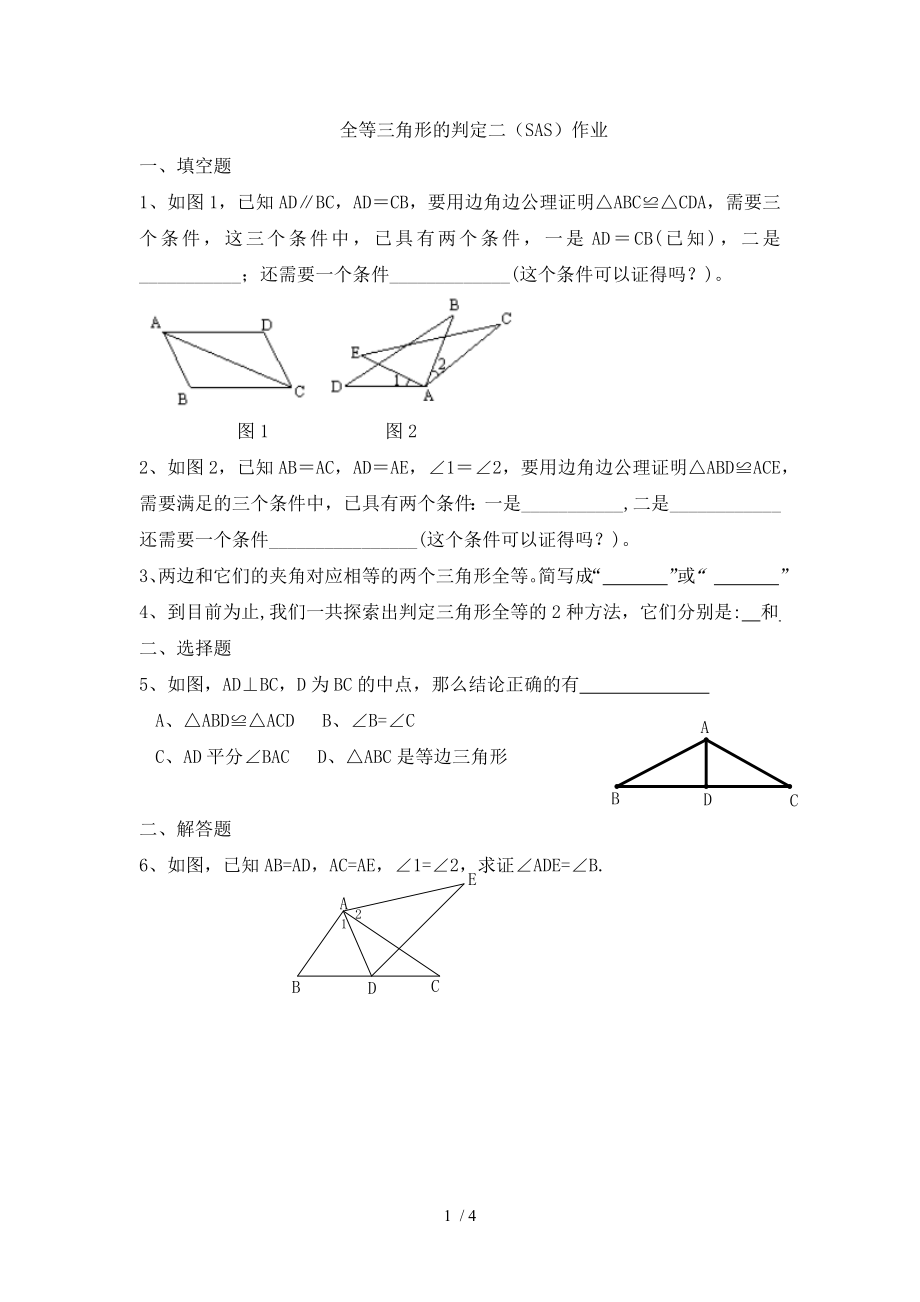
1、如圖1，已知AD∥BC，AD＝CB，要用邊角邊公理證明△ABC≌△CDA，需要三個條件，這三個條件中，已具有兩個條件，一是AD＝CB(已知)，二是___________；還需要一個條件_____________(這個條件可以證得嗎？)。
圖1 圖2
2、 如圖2，已知AB＝AC，AD＝AE，∠1＝∠2，要用邊角邊公理證明△ABD≌ACE，需要滿足的三個條件中，已具有兩個條件：一是___________,二是____________還需要一個條件________________(這個條件可以證得嗎？)。
3、兩邊和它
2、們的夾角對應(yīng)相等的兩個三角形全等。簡寫成“ ”或“ ”
4、到目前為止,我們一共探索出判定三角形全等的2種方法，它們分別是: 和
二、選擇題
5、如圖，AD⊥BC，D為BC的中點，那么結(jié)論正確的有
A、△ABD≌△ACD B、∠B=∠C
C、AD平分∠BAC D、△ABC是等邊三角形
二、解答題
6、如圖，已知AB=AD，AC=AE，∠1=∠2，求證∠ADE=∠B.
7、已知：如圖，AB＝AC，F(xiàn)、E分別是AB、AC的中點。求證：△ABE≌△ACF。
3、
8、已知：如圖，和相交于點，，。求證：。
9、已知：點A、F、E、C在同一條直線上， AF＝CE，BE∥DF，BE＝DF．
求證：△ABE≌△CDF．
10、如圖，△ABC中，AB＝AC，AD平分∠BAC，試說明△ABD≌△ACD。
11、已知：如圖， AD∥BC，AD=BC，AE=CF。求證：△AFD≌△CEB
12、如圖，在△ABC中，D是AB上一點，DF交AC于點E，DE=FE，AE=CE，AB與CF有什么位置關(guān)系？說明你判斷的理由。
4、
13、如圖，已知OA=OB,應(yīng)填什么條件就得到△AOC≌△BOD
(允許添加一個條件)
14、如圖，已知CA=CB,AD=BD,M、N分別是CA、CB的中點，求證：DM=DN
15、判斷下列各組中的兩個三角形是否全等，并說明理由.
(1)圖(1)中的△AEC與△ADB.已知條件是AB＝AC，AD＝AE.
(2)圖(2)中的△ABC與△BAD.已知條件是∠BAC＝∠ABD，AC＝BD.
(3)圖(3)中的△AEC與△ADB.已知條件是AB＝AC，AD＝AE，BE＝CD.
4 / 4
人教版八年級上冊數(shù)學(xué) 12.2全等三角形的判定（SAS）同步練習(xí)（無答案）
