2020-2021學(xué)年人教版 八年級(jí)數(shù)學(xué)上冊(cè) 第13.3 等腰三角形 同步訓(xùn)練

《2020-2021學(xué)年人教版 八年級(jí)數(shù)學(xué)上冊(cè) 第13.3 等腰三角形 同步訓(xùn)練》由會(huì)員分享，可在線閱讀，更多相關(guān)《2020-2021學(xué)年人教版 八年級(jí)數(shù)學(xué)上冊(cè) 第13.3 等腰三角形 同步訓(xùn)練（8頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

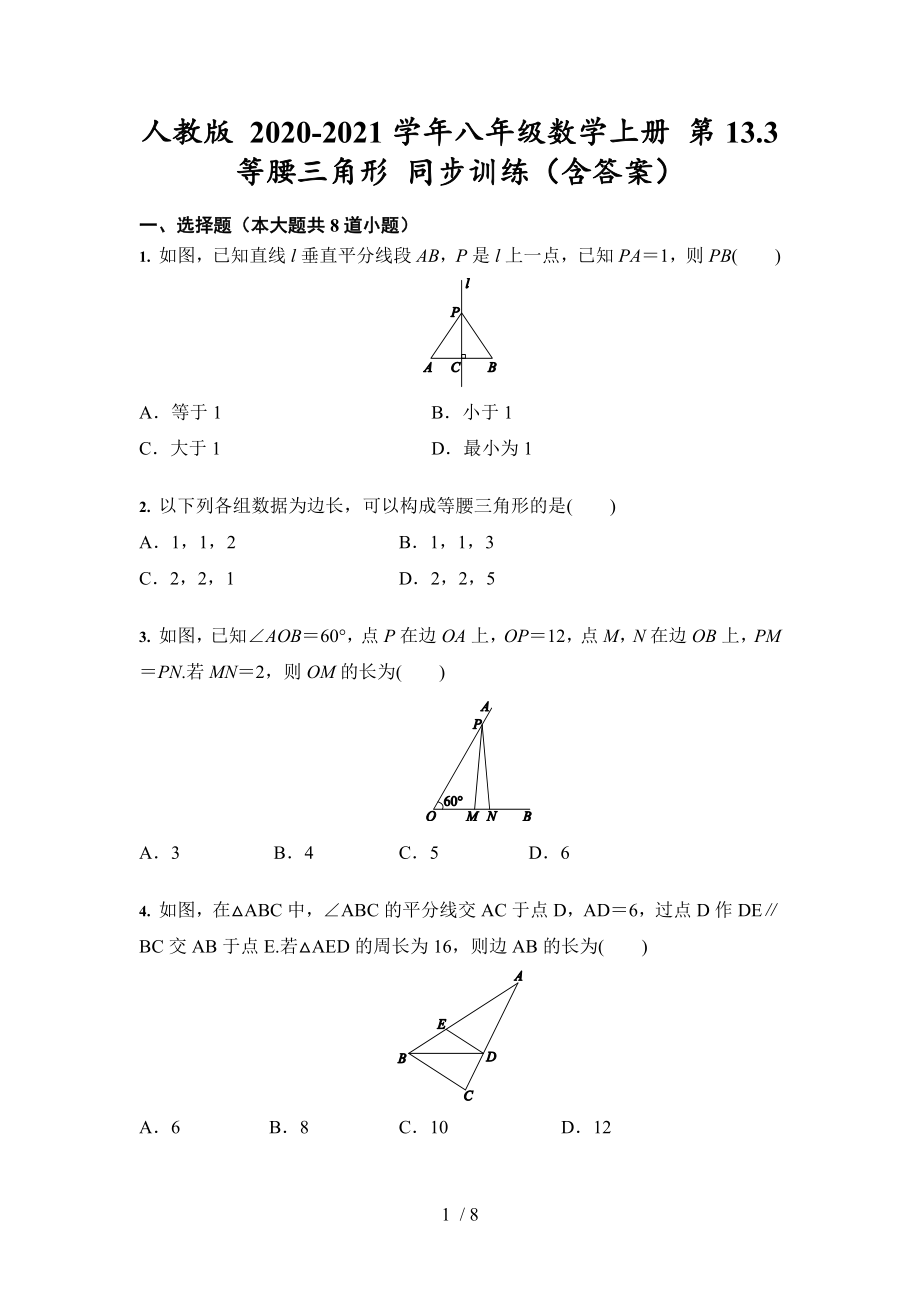
1、人教版 2020-2021學(xué)年八年級(jí)數(shù)學(xué)上冊(cè) 第13.3 等腰三角形 同步訓(xùn)練（含答案） 一、選擇題（本大題共8道小題） 1. 如圖，已知直線l垂直平分線段AB，P是l上一點(diǎn)，已知PA＝1，則PB(　　) A．等于1 B．小于1 C．大于1 D．最小為1 2. 以下列各組數(shù)據(jù)為邊長，可以構(gòu)成等腰三角形的是(　　) A．1，1，2 B．1，1，3 C．2，2，1 D．2，2，5 3. 如圖，已知∠AOB＝60°，點(diǎn)P在邊OA上，OP＝12，點(diǎn)M，N在邊OB上，PM＝PN.若MN＝2，則OM的長為(　　) 　　

2、 A．3 B．4 C．5 D．6 4. 如圖，在△ABC中，∠ABC的平分線交AC于點(diǎn)D，AD＝6，過點(diǎn)D作DE∥BC交AB于點(diǎn)E.若△AED的周長為16，則邊AB的長為(　　) A．6 B．8 C．10 D．12 5. 如圖，△ABC中，AB＝AC，AD是∠BAC的平分線，已知AB＝5，AD＝3，則BC的長為(　　) A. 5 B. 6 C. 8 D. 10 6. 如圖，△ABC是等邊三角形，AD⊥BC于點(diǎn)D，點(diǎn)E在AC上，且AE＝AD，則∠DEC的度數(shù)為(　　) A．105° B．95°

3、C．85° D．75° 7. 如圖，AD平分∠BAC，AD⊥BD于點(diǎn)D，DE∥AC，則圖中的等腰三角形有(　　) A．0個(gè) 　　 B．1個(gè) C．2個(gè) 　　 D．3個(gè) 8. 如圖，在△ABC中，過頂點(diǎn)A的直線DE∥BC，∠ABC，∠ACB的平分線分別交DE于點(diǎn)E，D.若AC＝3，AB＝4，則DE的長為(　　) A．6 B．7 C．8 D．9 二、填空題（本大題共4道小題） 9. 如圖，在△ABC中，AB＝AC，∠BAC＝40°，AD是中線，BE是高，AD與BE交于點(diǎn)F，則∠BFD＝________°.

4、 10. 如圖所示，在△ABC中，∠B＝50°，∠C＝90°，在射線BA上找一點(diǎn)D，使△ACD為等腰三角形，則∠ADC的度數(shù)為________． 11. 如圖，六邊形ABCDEF的六個(gè)內(nèi)角都相等．若AB＝1，BC＝CD＝3，DE＝2，則這個(gè)六邊形的周長為________． 12. 規(guī)律探究如圖，∠BOC＝9°，點(diǎn)A在OB上，且OA＝1，按下列要求畫圖： 以A為圓心，1為半徑向右畫弧交OC于點(diǎn)A1，得第1條線段AA1； 再以A1為圓心，1為半徑向右畫弧交OB于點(diǎn)A2，得第2條線段A1A2； 再以A2為圓心，1為半徑向右畫弧交OC于點(diǎn)A3，得第3條線段A2A3…… 這

5、樣畫下去，直到得第n條線段，之后就不能再畫出符合要求的線段了，則n＝________． 三、解答題（本大題共3道小題） 13. 如圖，在△ABC中，O是邊AC上的一個(gè)動(dòng)點(diǎn)，過點(diǎn)O作直線MN∥BC，設(shè)MN交∠BCA的平分線于點(diǎn)E，交△ABC的外角平分線于點(diǎn)F.探究線段OE與OF的數(shù)量關(guān)系，并說明理由． 14. 如圖，在等邊三角形ABC中，點(diǎn)D，E分別在邊BC，AC上，且DE∥AB，過點(diǎn)E作EF⊥DE，交BC的延長線于點(diǎn)F.求證：DF＝2DC. 15. 如圖①，在△ABC中，AB＝AC，P為底邊BC上一點(diǎn)，PE⊥AB，PF⊥AC，CH⊥

6、AB，垂足分別為E，F(xiàn)，H.易證PE＋PF＝CH.證明過程如下： 連接AP. ∵PE⊥AB，PF⊥AC，CH⊥AB， ∴S△ABP＝AB·PE，S△ACP＝AC·PF，S△ABC＝AB·CH. 又∵S△ABP＋S△ACP＝S△ABC， ∴AB·PE＋AC·PF＝AB·CH. ∵AB＝AC，∴PE＋PF＝CH. 如圖②，若P為BC延長線上的點(diǎn)，其他條件不變，PE，PF，CH之間又有怎樣的數(shù)量關(guān)系？請(qǐng)寫出你的猜想，并加以證明． 人教版 2020-2021學(xué)年八年級(jí)數(shù)學(xué)上冊(cè) 第13.3 等腰三角形 同步訓(xùn)練-答案 一、選擇題（本

7、大題共8道小題） 1. 【答案】A 2. 【答案】C 3. 【答案】C　[解析] 如圖，過點(diǎn)P作OB的垂線段，交OB于點(diǎn)D， 則△PDO為含30°角的直角三角形， ∴OD＝OP＝6. ∵PM＝PN，MN＝2，∴MD＝DN＝1. ∴OM＝OD－MD＝6－1＝5. 故選C. 4. 【答案】C　[解析] ∵BD平分∠ABC， ∴∠EBD＝∠CBD. ∵DE∥BC，∴∠EDB＝∠CBD. ∴∠EBD＝∠EDB.∴BE＝DE. ∵△AED的周長為16， ∴AE＋DE＋AD＝AE＋BE＋AD＝AB＋AD＝16. ∵AD＝6，∴AB＝10.

8、 5. 【答案】C　【解析】∵AB＝AC，AD平分∠BAC，∴根據(jù)等腰三角形三線合一性質(zhì)可知AD⊥BC，BD＝CD，在Rt△ABD中，AB＝5，AD＝3，由勾股定理得BD＝4，∴BC＝2BD＝8. 6. 【答案】A　[解析] ∵△ABC是等邊三角形，∴∠BAC＝60°.∵AD⊥BC，∴AD平分∠BAC.∴∠DAC＝30°.∵AD＝AE，∴∠ADE＝∠AED＝＝75°.∴∠DEC＝105°. 7. 【答案】C　[解析] 如圖所示． ∵DE∥AC，∴∠1＝∠3. ∵AD平分∠BAC，∴∠1＝∠2.∴∠2＝∠3.∴AE＝DE.∴△ADE是等腰三角形． ∵AD⊥BD，∴∠

9、2＋∠B＝90°，∠3＋∠BDE＝90°.∵∠2＝∠3，∴∠B＝∠BDE.∴BE＝DE.∴△BDE是等腰三角形． 8. 【答案】B　[解析] 由題意得∠EBC＝∠ABE，∠ACD＝∠DCB.根據(jù)平行線的性質(zhì)得∠DCB＝∠ADC，∠EBC＝∠AEB，所以∠ADC＝∠ACD，∠ABE＝∠AEB.所以AD＝AC，AB＝AE.所以DE＝AD＋AE＝AC＋AB＝3＋4＝7. 二、填空題（本大題共4道小題） 9. 【答案】70 10. 【答案】20°或70°或100°　[解析] 如圖，有三種情形： ①當(dāng)AC＝AD時(shí)，∠ADC＝70°； ②當(dāng)CD′＝AD′時(shí)，∠AD′

10、C＝100°； ③當(dāng)AC＝AD″時(shí)，∠AD″C＝20°. 11. 【答案】15　[解析] 由多邊形的內(nèi)角和定理可知，這個(gè)六邊形的每個(gè)內(nèi)角都是120°，因此直線AB，CD，EF圍成一個(gè)等邊三角形，且這個(gè)等邊三角形的邊長為7.因此AF＝4，EF＝2.所以這個(gè)六邊形的周長＝1＋3＋3＋2＋2＋4＝15. 12. 【答案】9 三、解答題（本大題共3道小題） 13. 【答案】 解：OE＝OF. 理由：∵M(jìn)N∥BC， ∴∠OEC＝∠BCE，∠OFC＝∠DCF. ∵CE平分∠ACB，CF平分∠ACD， ∴∠OCE＝∠BCE，∠OCF＝∠DCF. ∴∠OEC＝∠O

11、CE，∠OFC＝∠OCF. ∴OE＝OC，OC＝OF.∴OE＝OF. 14. 【答案】 證明：∵△ABC是等邊三角形， ∴∠A＝∠B＝∠ACB＝60°. ∵DE∥AB， ∴∠EDC＝∠B＝60°，∠DEC＝∠A＝60°. ∵EF⊥DE，∴∠DEF＝90°. ∴∠F＝90°－∠EDC＝30°. ∵∠ACB＝∠EDC＝∠DEC＝60°， ∴△EDC是等邊三角形．∴DE＝DC. ∵∠DEF＝90°，∠F＝30°， ∴DF＝2DE＝2DC. 15. 【答案】 解：PE＝PF＋CH.證明如下： 連接AP. ∵PE⊥AB，PF⊥AC，CH⊥AB， ∴S△ABP＝AB·PE，S△ACP＝AC·PF，S△ABC＝AB·CH.∵S△ABP＝S△ACP＋S△ABC， ∴AB·PE＝AC·PF＋AB·CH. ∵AB＝AC，∴PE＝PF＋CH. 8 / 8