《(新課程)高中數(shù)學(xué) 2.3《函數(shù)的應(yīng)用(Ⅰ)》學(xué)案2 新人教B版必修1》由會員分享����,可在線閱讀,更多相關(guān)《(新課程)高中數(shù)學(xué) 2.3《函數(shù)的應(yīng)用(Ⅰ)》學(xué)案2 新人教B版必修1(4頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1、2.3 函數(shù)的應(yīng)用(一)學(xué)案
【預(yù)習(xí)達(dá)標(biāo)】
1.形如f(x)= 叫一次函數(shù)�����,當(dāng) 為增函數(shù)���;當(dāng)為減函數(shù)��。
2.二次函數(shù)的解析式三種常見形式為 �����;
�; 。
3.f(x)=a+bx+c(a0)�,當(dāng)a 0,其圖象開口向 ,函數(shù)有最 值,為 �;
當(dāng)a 0, 其圖象開口向 ,函數(shù)有最 值,為 �����。(當(dāng)給定一區(qū)間的二次函數(shù)的最值問題怎樣考慮����?)
4. f(x)=a+bx+c(a0)當(dāng)a>0時
2、,增區(qū)間為 ��;減區(qū)間為 .
【典例解析】
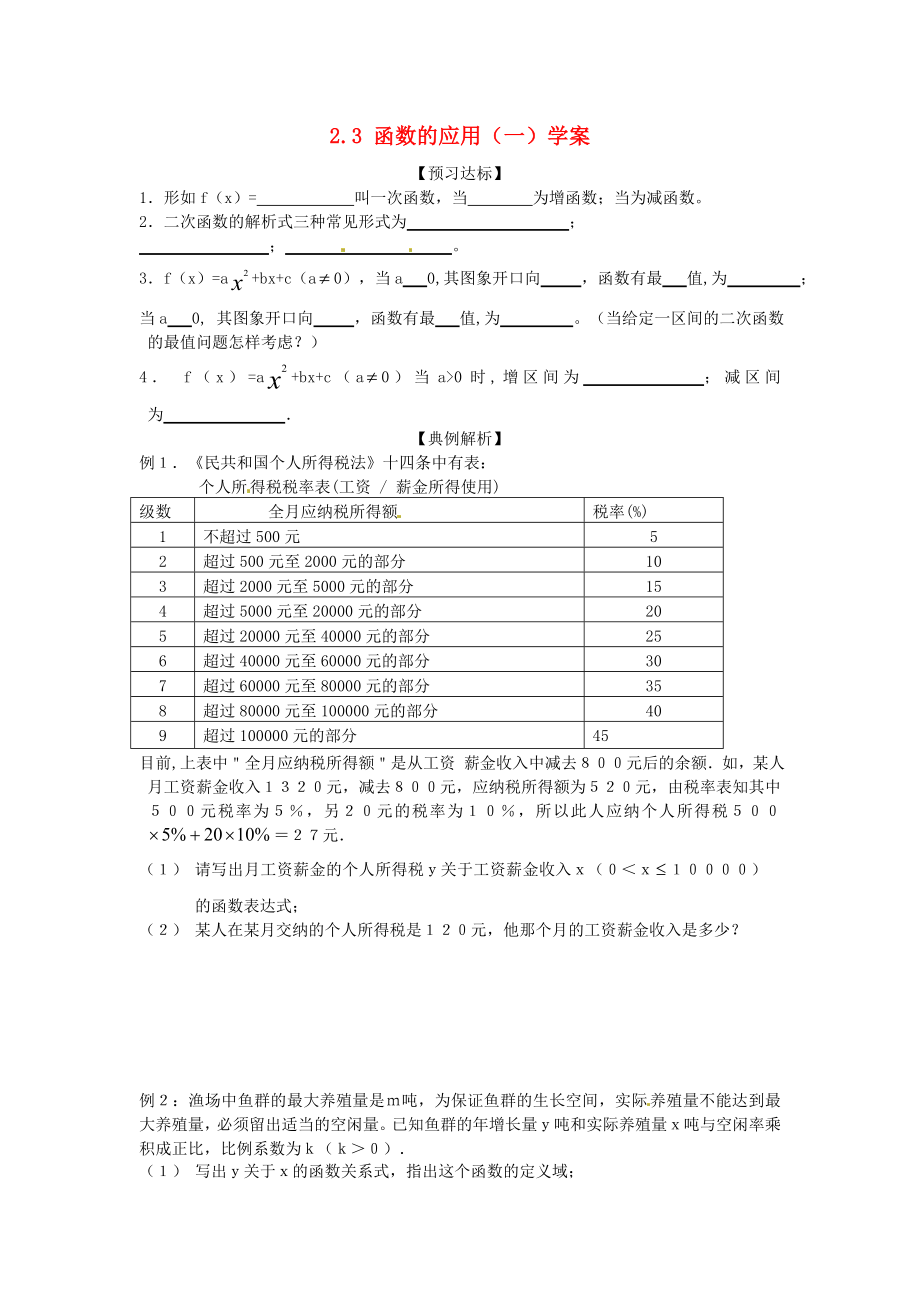
例1.《民共和國個人所得稅法》十四條中有表:
個人所得稅稅率表(工資 / 薪金所得使用)
級數(shù)
全月應(yīng)納稅所得額
稅率(%)
1
不超過500元
5
2
超過500元至2000元的部分
10
3
超過2000元至5000元的部分
15
4
超過5000元至20000元的部分
20
5
超過20000元至40000元的部分
25
6
超過40000元至60000元的部分
30
7
超過60000元至80000元的部分
35
8
超過80000元至100
3�、000元的部分
40
9
超過100000元的部分
45
目前,上表中"全月應(yīng)納稅所得額"是從工資 薪金收入中減去800元后的余額.如�,某人月工資薪金收入1320元,減去800元���,應(yīng)納稅所得額為520元�����,由稅率表知其中500元稅率為5%�,另20元的稅率為10%,所以此人應(yīng)納個人所得稅500=27元.
(1) 請寫出月工資薪金的個人所得稅y關(guān)于工資薪金收入x(0<x10000)的函數(shù)表達(dá)式�����;
(2) 某人在某月交納的個人所得稅是120元�����,他那個月的工資薪金收入是多少�����?
例2:漁場中魚群的最大養(yǎng)殖量是m噸����,為保證魚群的生長空間,實際養(yǎng)殖量不能達(dá)到最大養(yǎng)殖量���,
4����、必須留出適當(dāng)?shù)目臻e量。已知魚群的年增長量y噸和實際養(yǎng)殖量x噸與空閑率乘積成正比�,比例系數(shù)為k(k>0).
(1) 寫出y關(guān)于x的函數(shù)關(guān)系式,指出這個函數(shù)的定義域�;
(2) 求魚群年增長量的最大值;
(3) 當(dāng)魚群的年增長量達(dá)到最大值時���,求k的取值范圍.
例3:某摩托車生產(chǎn)企業(yè)�,上年度生產(chǎn)摩托車的投入成本為1萬元/輛���,出廠價為1.2萬元/輛�����,年銷量為1000�����。為適應(yīng)市場需求����,計劃提高產(chǎn)品檔次,適度增加投入成本�,若每輛車投入成本增加的比例為x(0<x<1=�����,則出廠價相應(yīng)的提高比例為0.75x����,同時預(yù)計年銷售量增加的比例為0.6,利潤=(出廠價-投入成本)年銷售量�����。
(1)
5�、 寫出本年度預(yù)計的年利潤y與投入成本增加的比例x的關(guān)系式;
(2) 為使本年度的年利潤比上年有說增加���,問投入成本增加的比例x應(yīng)在什么范圍�?
【當(dāng)堂練習(xí)】
1.某種電熱水器的水箱盛滿水時200升����,加熱到一定溫度即可浴用,浴用前�,已知每分鐘放水34升,在放水的同時按毫升/秒2的勻加速自動注水(即分鐘自動注水升)當(dāng)水箱內(nèi)的水達(dá)到最小值時����,放水過程自動停止.現(xiàn)假定每人洗浴用量為65升�,則該熱水器一次至多可供多少人洗?��。ā ����。?
A.3?����。拢础�����。茫怠�����。模?
2.?dāng)M定從甲地到乙地通話m分鐘的電話費由f(m)=1.06(0.5[m]+1)?�。ㄔQ定��,其中m>0,[m]是大于或等于m的最
6�、小整數(shù),則從甲地到乙地通話時間為5.5分鐘的電話費為( ?����。?
A.3.71元 ?�。拢?.97元 ?��。茫?.24元 D.4.77元
3.在測量某物理量的過程中�,因儀器和觀察的誤差,使得n次測量分別得到�,某n個數(shù)據(jù),我們規(guī)定所測物理量的"最佳近似值"a是這樣一個量:a與其它近似值相比較����,與各數(shù)據(jù)的差的平方和最小,依次規(guī)定�����,從推出的a= ?���。?
4.甲乙兩地相距s千米��,汽車從甲地勻速行駛到乙地���,速度不得超過c千米/小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分組成:可變部分與速度v的平方成正比�,其系數(shù)為b,固定部分為a元��,為了使全程運輸成本最低��,汽
7��、車應(yīng)以多大速度行駛�����?
5�����、(12分)某種商品現(xiàn)在定價每年p元��,每月賣出n件�����,因而現(xiàn)在每月售貨總金額np元,設(shè)定價上漲x成(1成=10%)��,賣出數(shù)量減少y成����,售貨總金額變成現(xiàn)在的z倍.
(1)用x和y表示z;(2)若y=x�����,求使售貨總金額有所增加的x值的范圍.
參考答案:
【預(yù)習(xí)達(dá)標(biāo)】 ?��。保耄猓ǎ耄埃唬耄荆?;k<0.
2.f(x)=a+bx+c;f(x)=a+k
8���、�����;f(x)=a(x-?����。ǎ幔埃常?����,上��,?��?���;<����,下,大.?�。矗郏?���;(-,-)
【典例解析】
例1��、解析:(1)應(yīng)納稅所得額為全月工資薪金總收入x-800元.
所以得:y=
(2)當(dāng)y=120時,y應(yīng)歸為:當(dāng)x(1800����,2800)時,y=25+(x-1300)10%
?。玻担ǎ保常埃埃保埃ィ剑保玻?
x=950+1300=2250(元)
評析:求分段函數(shù)的解析式關(guān)鍵在自變量按什么意義分段的.本題若設(shè)應(yīng)納稅所得額為x����,求應(yīng)納稅額f(x)隨應(yīng)納稅所得額x的函數(shù)關(guān)系是什么?
例2�����、解:(1)因魚群最大養(yǎng)殖量為m噸�����,實際養(yǎng)殖量為m噸�,則空閑量為(m-x)
9�、噸,空閑率為�,依題意,魚群增長量為y=kx(1-)定義域為(0<x<m)
(2)當(dāng)x=m/2時��,即魚群年增長量的最大值為.
(3)由于實際養(yǎng)殖量和年增長量之和小于最大養(yǎng)殖量,有0<x+y<m成立��,即0<�,得-2<k<2,但k>0�����,0<k<2.
評析:由于是二次函數(shù)��,處理最值問題時可依二次函數(shù)求最值得方法來求�����,而實際養(yǎng)殖量和年增長量之和小于最大養(yǎng)殖量應(yīng)是常識�����,在閱讀題意時要得到這個隱含條件.
例3�、(1)由題意得:y=[1.2]整理得y=-60.
(2)要保證本年度的利潤比上年度與所增加,當(dāng)且僅當(dāng)
即解不等式���,得0<x<
答:為保證本年度的年利潤比上年度有所增加�����,投入成本增加的比例應(yīng)滿足0<x<.
評析:建立模型后在用一元二次函數(shù)知識處理問題.
【當(dāng)堂練習(xí)】
1.B?�。玻谩����。常?
4.解:成本:y=s(+bv),v(0�,c,即為求f(v)=
s(+bv)=sb(v+)在(0���,c)上的最小值.
有定義易證得f(v)在(0����,)上遞減����,在[,+)上遞增�����,需討論c和的大?����。?
當(dāng)c時���,=f(c)�,此時v=c��;當(dāng)c時����,=f(),此時v=.
5. 解:(1)npz=p(1+)·n(1-)
∴z=
(2)當(dāng)y=x時���,z=
由z>1���,得>1
x(x-5)<0,∴0<x<5���。
 (新課程)高中數(shù)學(xué) 2.3《函數(shù)的應(yīng)用(Ⅰ)》學(xué)案2 新人教B版必修1
(新課程)高中數(shù)學(xué) 2.3《函數(shù)的應(yīng)用(Ⅰ)》學(xué)案2 新人教B版必修1