《2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀(guān)題專(zhuān)練 立體幾何(10) 文》由會(huì)員分享�����,可在線(xiàn)閱讀���,更多相關(guān)《2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀(guān)題專(zhuān)練 立體幾何(10) 文(8頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1��、立體幾何(10)
一���、選擇題(本題共12小題����,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中��,只有一項(xiàng)是符合題目要求的)
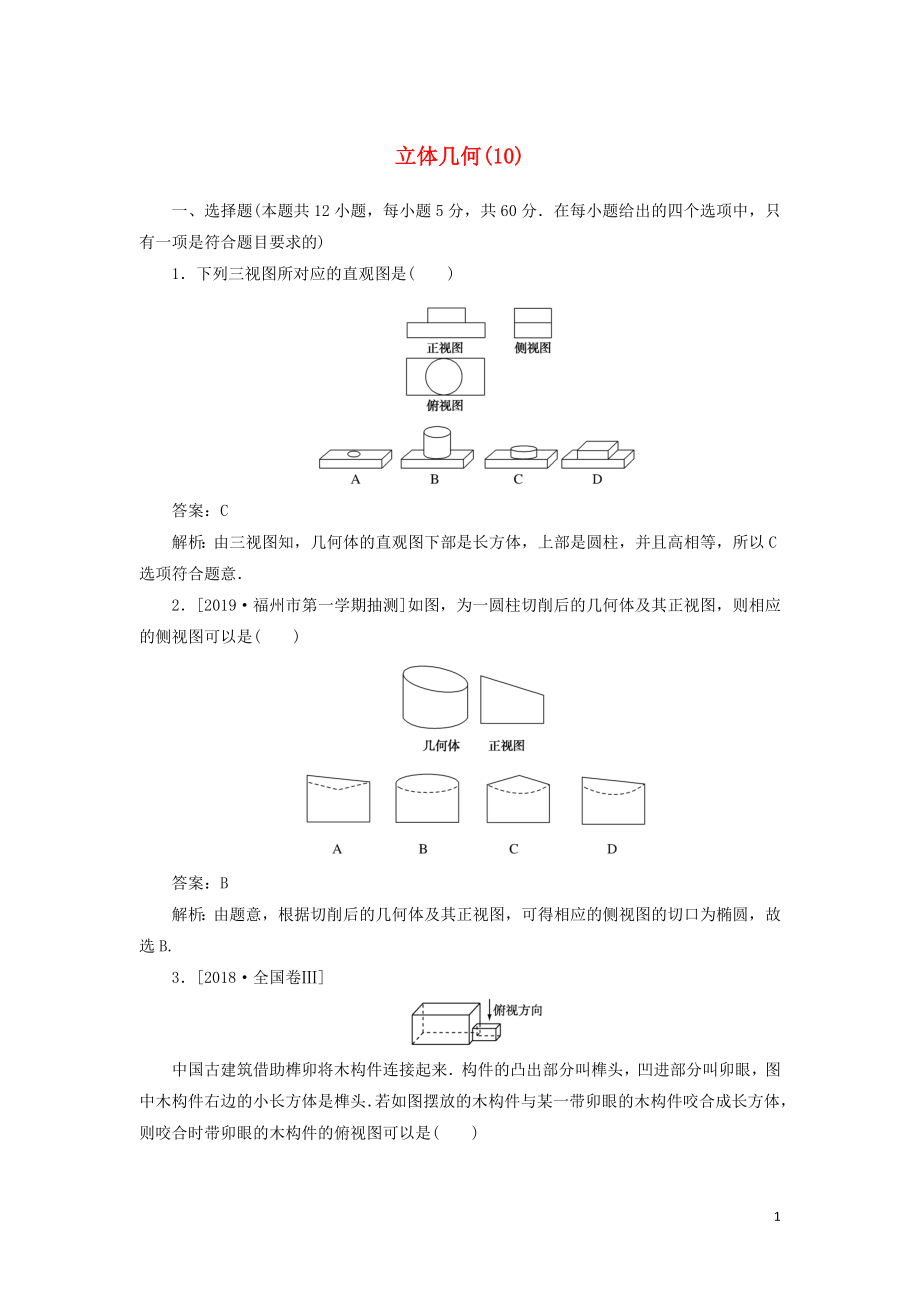
1.下列三視圖所對(duì)應(yīng)的直觀(guān)圖是( )
答案:C
解析:由三視圖知�����,幾何體的直觀(guān)圖下部是長(zhǎng)方體�����,上部是圓柱����,并且高相等�,所以C選項(xiàng)符合題意.
2.[2019·福州市第一學(xué)期抽測(cè)]如圖,為一圓柱切削后的幾何體及其正視圖���,則相應(yīng)的側(cè)視圖可以是( )
答案:B
解析:由題意���,根據(jù)切削后的幾何體及其正視圖��,可得相應(yīng)的側(cè)視圖的切口為橢圓�,故選B.
3.[2018·全國(guó)卷Ⅲ]
中國(guó)古建筑借助榫卯將木構(gòu)件連接起來(lái).構(gòu)件的凸出部分叫榫頭�,凹進(jìn)部分叫卯眼,圖中
2����、木構(gòu)件右邊的小長(zhǎng)方體是榫頭.若如圖擺放的木構(gòu)件與某一帶卯眼的木構(gòu)件咬合成長(zhǎng)方體,則咬合時(shí)帶卯眼的木構(gòu)件的俯視圖可以是( )
A
B
C
D
答案:A
解析:
由題意可知帶卯眼的木構(gòu)件的直觀(guān)圖如圖所示��,由直觀(guān)圖可知其俯視圖應(yīng)選A.
故選A.
4.[2019·桂林�����、百色��、崇左市聯(lián)合模擬]如圖�,在正方體ABCD-A1B1C1D1中,E為棱BB1的中點(diǎn)�����,用平面AEC1截去該正方體的上半部分�����,則剩余幾何體的正(主)視圖為( )
答案:B
解析:因?yàn)锳BCD-A1B1C1D1是正方體,所以AE∥平面DCC1D1��,設(shè)平面AEC1∩平面DCC1D1=C1G���,
3����、因?yàn)锳E?平面AEC1�,所以AE∥C1G,AE=C1G.取CC1的中點(diǎn)F����,連接EF,DF�����,易得四邊形AEFD為平行四邊形���,所以AE∥DF,AE=DF�,所以C1G∥DF,C1G=DF���,所以G為DD1的中點(diǎn)�����,連接AG�,則平面AEC1G即平面AEC1截正方體所得的截面,則剩余的幾何體為 A1B1C1D1GAE��,所以易得其正視圖如選項(xiàng)B所示�,故選B.
5.[2019·武漢調(diào)研]某幾何體的三視圖如圖所示,則從該幾何體的所有頂點(diǎn)中任取兩個(gè)頂點(diǎn)�����,它們之間距離的最大值為( )
A. B.
C.2 D.2
答案:B
解析:
由三視圖知����,該幾何體是一個(gè)四棱柱,記為四棱柱ABCD-A1B1
4��、C1D1�,將其放在如圖所示的長(zhǎng)方體中,底面ABCD是邊長(zhǎng)為1的正方形��,四棱柱的高為1,連接AC1�����,觀(guān)察圖形可知�,幾何體中兩頂點(diǎn)間距離的最大值為AC1的長(zhǎng),即=.故選B.
6.設(shè)一個(gè)球形西瓜�����,切下一刀后所得切面圓的半徑為4���,球心到切面圓心的距離為3���,則該西瓜的體積為( )
A.100π B.π
C.π D.π
答案:D
解析:因?yàn)榍忻鎴A的半徑r=4,球心到切面的距離d=3�����,所以球的半徑R===5����,故球的體積V=πR3=π×53=π��,即該西瓜的體積為π.
7.[2019·昆明市質(zhì)量檢測(cè)]一個(gè)幾何體的三視圖如圖所示,則該幾何體的體積為( )
A.4+ B.4+
C.12
5��、+ D.12+
答案:C
解析:三視圖對(duì)應(yīng)的幾何體是一個(gè)半球與一個(gè)長(zhǎng)方體的組合體�����,半球的半徑為1�,體積為;長(zhǎng)方體的長(zhǎng)�、寬、高分別為2�����、2��、3�����,體積為12.所以組合體的體積為12+.故選C.
8.[2019·廣東省七校聯(lián)考]某幾何體的三視圖如圖所示�����,則該幾何體的表面積和體積分別是( )
A.24+6和40 B.24+6和72
C.64+6和40 D.64+6和72
答案:C
解析:
把三視圖還原成幾何體���,如圖所示.由題意知S四邊形ABCD=12�,S四邊形BCC1B1=8,S四邊形ABB1A1=6���,S四邊形ADSA1=(2+6)×4×=16�����,S四邊形DCC1S=(2
6���、+6)×3×=12.易得B1A1⊥SA1,B1C1⊥SC1�����,且SA1=4����,SC1=5,所以S△SA1B1=3×4×=6�,S△SB1C1=4×5×=10,所以該幾何體的表面積為12+8+6+16+12+6+10=64+6.在棱SD上取一點(diǎn)D1����,使得DD1=2���,連接A1D1�,C1D1,則該幾何體的體積V=VS-A1B1C1D1+VABCD-A1B1C1D1=×12×4+12×2=40��,故選C.
9.[2019·廣州市綜合檢測(cè)(一)]一個(gè)幾何體的三視圖如圖所示��,其中正視圖和俯視圖中的四邊形是邊長(zhǎng)為2的正方形��,則該幾何體的表面積為( )
A. B.7π
C. D.8π
答案:B
解
7�����、析:由三視圖可知該幾何體是一個(gè)圓柱體和一個(gè)球體的四分之一的組合體���,則所求的幾何體的表面積為×4π×12+π×12+π×12+2π×1×2=7π�,選B.
10.[2019·蓉城名校第一次聯(lián)考]已知一個(gè)幾何體的正視圖和側(cè)視圖如圖1所示�����,其俯視圖用斜二測(cè)畫(huà)法所畫(huà)出的水平放置的直觀(guān)圖是一個(gè)直角邊長(zhǎng)為1的等腰直角三角形(如圖2所示)����,則此幾何體的體積為( )
A.1 B.
C.2 D.2
答案:B
解析:
根據(jù)直觀(guān)圖可得該幾何體的俯視圖是一個(gè)直角邊長(zhǎng)分別是2和的直角三角形(如圖所示)��,根據(jù)三視圖可知該幾何體是一個(gè)三棱錐����,且三棱錐的高為3���,所以體積V=××3=.故選B.
11.
8�、古人采用“用臼舂米”的方法脫去稻谷的外殼���,獲得可供食用的大米�,用于舂米的“臼”多用石頭或木頭制成.一個(gè)“臼”的三視圖如圖所示��,則鑿去部分(看成一個(gè)簡(jiǎn)單的組合體)的體積為( )
A.63π B.72π
C.79π D.99π
答案:A
解析:由三視圖得鑿去部分是圓柱與半球的組合體��,其中圓柱的高為5�����,底面圓的半徑為3��,半球的半徑為3�����,所以組合體的體積為π×32×5+×π×33=63π.
12.已知三棱錐P-ABC的四個(gè)頂點(diǎn)都在球O的表面上,PA⊥平面ABC����,AB⊥BC,且PA=8.若平面ABC截球O所得截面的面積為9π�����,則球O的表面積為( )
A.10π B.25π
C
9�����、.50π D.100π
答案:D
解析:設(shè)球O的半徑為R�����,由平面ABC截球O所得截面的面積為9π��,得△ABC的外接圓的半徑為3.設(shè)該外接圓的圓心為D����,因?yàn)锳B⊥BC���,所以點(diǎn)D為AC的中點(diǎn)��,所以DC=3.因?yàn)镻A⊥平面ABC��,易證PB⊥BC�����,所以PC為球O的直徑.又PA=8���,所以O(shè)D=PA=4���,所以R=OC==5,
所以球O的表面積為S=4πR2=100π.
二�����、填空題(本題共4小題�����,每小題5分��,共20分)
13.[2019·長(zhǎng)春市質(zhì)量監(jiān)測(cè)(一)]已知一所有棱長(zhǎng)都是的三棱錐��,則該三棱錐的體積為_(kāi)_______.
答案:
解析:記所有棱長(zhǎng)都是的三棱錐為P-ABC,如圖所示�����,取B
10�����、C的中點(diǎn)O�����,連接AD��,PD��,作PO⊥AD于點(diǎn)O�,則PO⊥平面ABC����,且OP=×=,故三棱錐P-ABC的體積V=S△ABC·OP=××()2×=.
14.如圖��,在正三棱柱ABC-A1B1C1中���,D為棱AA1的中點(diǎn).若AA1=4�����,AB=2�,則四棱錐B-ACC1D的體積為_(kāi)_______.
答案:2
解析:取AC的中點(diǎn)O,連接BO(圖略)�����,則BO⊥AC�,所以BO⊥平面ACC1D.
因?yàn)锳B=2,所以BO=.
因?yàn)镈為棱AA1的中點(diǎn)��,AA1=4����,所以AD=2,
所以S梯形ACC1D=×(2+4)×2=6��,所以四棱錐B-ACC1D的體積為×6×=2.
15.如圖��,半徑為4的球O中有一內(nèi)
11��、接圓柱��,則圓柱的側(cè)面積最大值是________.
答案:32π
解析:設(shè)圓柱的上底面半徑為r,球的半徑與上底面夾角為α���,則r=4cos α��,圓柱的高為8sin α.
所以圓柱的側(cè)面積為32πsin 2α.
當(dāng)且僅當(dāng)α=時(shí)�����,sin 2α=1��,圓柱的側(cè)面積最大�,
所以圓柱的側(cè)面積的最大值為32π.
16.[2019·江西省五校協(xié)作體試題]某幾何體的三視圖如圖所示��,正視圖是一個(gè)上底為2�����,下底為4的直角梯形�,俯視圖是一個(gè)邊長(zhǎng)為4的等邊三角形����,則該幾何體的體積為_(kāi)___________.
答案:
解析:把三視圖還原成幾何體ABC-DEF,如圖所示���,在A(yíng)D上取點(diǎn)G����,使得AG=2,連接GE��,GF���,則把幾何體ABC-DEF分割成三棱柱ABC-GEF和三棱錐D-GEF����,所以VABC-DEF=VABC-GEF+VD-GEF=4×2+×4×2=.
8
 2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀(guān)題專(zhuān)練 立體幾何(10) 文
2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀(guān)題專(zhuān)練 立體幾何(10) 文