《2014-2015學年高中數(shù)學(人教A版必修四) 第二章 平面向量 章末復習課2 課時作業(yè)(含答案)》由會員分享��,可在線閱讀����,更多相關(guān)《2014-2015學年高中數(shù)學(人教A版必修四) 第二章 平面向量 章末復習課2 課時作業(yè)(含答案)(5頁珍藏版)》請在裝配圖網(wǎng)上搜索。
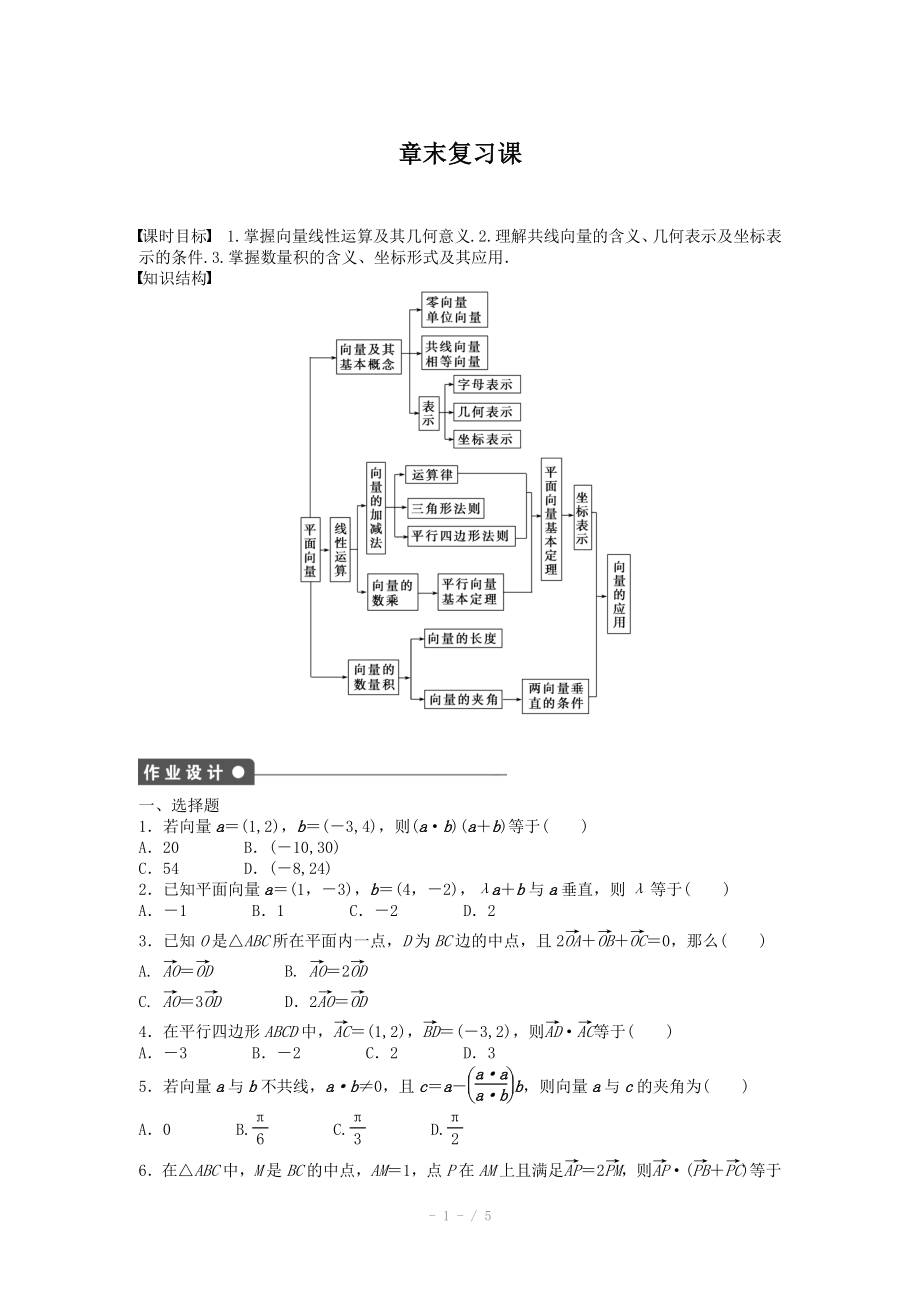
1����、 - 1 - / 5 章末復習課章末復習課 課時目標 1.掌握向量線性運算及其幾何意義.2.理解共線向量的含義、 幾何表示及坐標表示的條件.3.掌握數(shù)量積的含義�����、坐標形式及其應(yīng)用 知識結(jié)構(gòu) 一�����、選擇題 1若向量a a(1,2),b b(3,4)���,則(a ab b)(a ab b)等于( ) A20 B(10,30) C54 D(8,24) 2已知平面向量a a(1,3)���,b b(4,2)����,a ab b與a a垂直,則等于( ) A1 B1 C2 D2 3已知O是ABC所在平面內(nèi)一點�����,D為BC邊的中點�,且 2OAOBOC0,那么( ) A. AOOD B. AO2OD C. AO3OD D2AO
2���、OD 4在平行四邊形ABCD中��,AC(1,2)��,BD(3,2)����,則ADAC等于( ) A3 B2 C2 D3 5若向量a a與b b不共線,abab0��,且c ca aaaaaababb b��,則向量a a與c c的夾角為( ) A0 B.6 C.3 D.2 6在ABC中�,M是BC的中點,AM1��,點P在AM上且滿足AP2PM����,則AP(PBPC)等于 - 2 - / 5 ( ) A.49 B.43 C43 D49 題 號 1 2 3 4 5 6 答 案 二、填空題 7過點A(2,3)且垂直于向量a a(2,1)的直線方程是_ 8已知向量a a���,b b滿足|a a|1����,|b b|2�,a a與b b的夾
3、角為 60,則b b在a a上的投影是_ 9 設(shè)向量a a(1,2)�����,b b(2,3) 若向量a ab b與向量c c(4�����, 7)共線��, 則_. 10 已知平面向量�、, |1�����, |2�����,(2)�, 則|2|的值是_ 三��、解答題 11已知A(1��,2)、B(2,1)��、C(3,2)和D(2,3)����,以AB、AC為一組基底來表示ADBDCD. 12設(shè)a a��,b b是兩個不共線的非零向量�����,tR R. (1)若a a與b b起點相同��,t為何值時a a�,tb b,13(a ab b)三向量的終點在一直線上���? (2)若|a a|b b|且a a與b b夾角為 60�����,那么t為何值時��,|a atb b|的值最?���。?能力
4�����、提升 13已知點O為ABC所在平面內(nèi)一點�,且OA2BC2OB2CA2OC2AB2,則O一定是ABC的( ) A外心 B內(nèi)心 C垂心 D重心 14. 如圖����, 平面內(nèi)有三個向量OA、OB�����、OC����, 其中OA與OB的夾角為 120����,OA與OC的夾角為 30,且|OA|OB|1����,|OC|2 3.若OCOAOB(�,R R)�����,求實數(shù)�����、的值 - 3 - / 5 1由于向量有幾何法和坐標法兩種表示方法�����,它的運算也因為這兩種不同的表示方法而有兩種方式���,因此向量問題的解決�����,理論上講總共有兩個途徑即基于幾何表示的幾何法和基于坐標表示的代數(shù)法����,在具體做題時要善于從不同的角度考慮問題 2向量是一個有“形”的幾何量��,因此,
5�、在研究向量的有關(guān)問題時,一定要結(jié)合圖形進行分析判斷求解��,這是研究平面向量最重要的方法與技巧 章末復習課章末復習課 答案答案 作業(yè)設(shè)計 1B a ab b385�����,a ab b(2,6)���, (a ab b)(a ab b)5(2,6)(10,30)故選 B. 2A (a ab b)a a0���,a a2a ab b0. 10100,1.故選 A. 3A 由題意D是BC邊的中點��, 所以有OBOC2OD����, 所以 2OAOBOC2OA2OD2(OAOD)0OAOD0AOOD. 4D ACABAD(1,2),BDADAB(3,2)�,解得AD(1,2),ADAC(1,2)(1,2)3.故選 D. 5D acac
6�、aa a aaaaaababb baaaaaaaaabab(abab)0��,a a,c c2. 6A 易知P為ABC的重心��,則PBPCPAAP�����,故AP(PBPC)AP249����,故選 A. 72xy70 解析 設(shè)直線上任一點P(x,y)�����,則AP(x2��,y3) 由APa a2(x2)(y3)0���,得 2xy70. 81 解析 b b在a a上的投影為|b b|cos 2cos 601. 92 解析 a ab b(2,23)與c c(4���,7)共線, (2)(7)(23)(4)0����,得2. 10. 10 解析 由(2)得(2)0�, 220.又|1�, 12.又|2, - 4 - / 5 |2|22 424244
7���、124 10. 11解 AB(1,3)����,AC(2,4)���,AD(3,5)�, BD(4,2)����,CD(5,1), ADBDCD(3,5)(4,2)(5,1)(12,8) 根據(jù)平面向量基本定理���,必存在唯一實數(shù)對m�,n使得 ADBDCDmABnAC����, (12,8)m(1,3)n(2,4) 12m2n,83m4n.��,得m32,n22. ADBDCD32AB22AC. 12解 (1)設(shè)a atb bma a13(a ab b)����,mR R��, 化簡得(23m1)a a(m3t)b b���, a a與b b不共線���, 23m10m3t0, m32�����,t12. t12時����,a a,tb b��,13(a ab b)的終點在一直線
8���、上 (2)|a atb b|2(a atb b)2|a a|2t2|b b|22t|a a|b b|cos 60(1t2t)|a a|2. 當t12時�,|a atb b|有最小值32|a a|. 13C 由OA2BC2OB2CA2,得OA2(OCOB)2OB2(OAOC)2�,得OCOBOAOC.OCAB0,O在邊AB的高線上同理O在邊AC的高線上�,即O為ABC的垂心故選 C. 14解 方法一 過點C分別作平行于OB的直線CE交直線OA于點E, 平行于OA的直線CF交直線OB于點F.如圖所示 在 RtOCE中���,|OE|OC|cos 302 3324�; |CE|OC|tan 302 3332����, 由平行四邊形法則知,OCOEOF4OA2OB��, - 5 - / 5 4�,2. 方法二 如圖所示,以O(shè)A所在直線為x軸�,過O垂直于OA的直線為y軸建立直角坐標系設(shè)B點在x軸的射影為B,C點在x軸的射影為C. 易知���,OC2 3cos 303�����,CCOCsin 30 3���,BBOBsin 6032��, OBOBcos 6012���, A點坐標為(1,0)�����,B點坐標為12���,32�����, C點坐標為(3�����, 3) OCOAOB 123�,032 3����, 42. 方法三 OCOAOB. OCOCOAOBOCOAOCOAOBOA��, 2 3321222 332����,解得4�,2.
 2014-2015學年高中數(shù)學(人教A版必修四) 第二章 平面向量 章末復習課2 課時作業(yè)(含答案)
2014-2015學年高中數(shù)學(人教A版必修四) 第二章 平面向量 章末復習課2 課時作業(yè)(含答案)