《2018年七年級(jí)升八年級(jí)數(shù)學(xué) 暑期銜接班講義 第二十講 專(zhuān)題七 綜合題題型專(zhuān)題訓(xùn)練(無(wú)答案) 新人教版》由會(huì)員分享,可在線閱讀��,更多相關(guān)《2018年七年級(jí)升八年級(jí)數(shù)學(xué) 暑期銜接班講義 第二十講 專(zhuān)題七 綜合題題型專(zhuān)題訓(xùn)練(無(wú)答案) 新人教版(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1����、
第二十講:專(zhuān)題七:綜合題題型專(zhuān)題訓(xùn)練
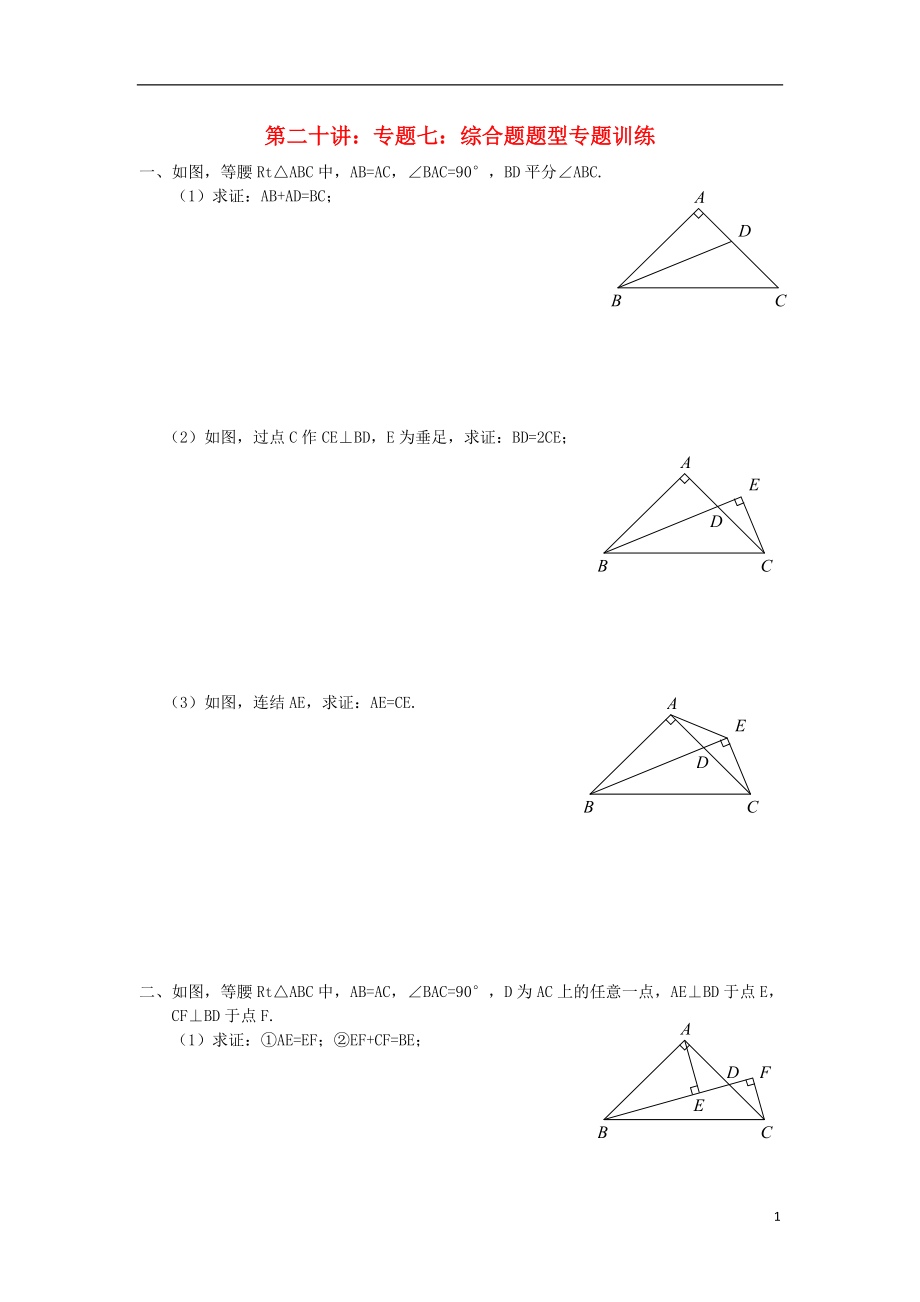
一、如圖�,等腰Rt△ABC中,AB=AC��,∠BAC=90°����,BD平分∠ABC.
(1)求證:AB+AD=BC;
(2)如圖�,過(guò)點(diǎn)C作CE⊥BD,E為垂足�,求證:BD=2CE;
(3)如圖��,連結(jié)AE,求證:AE=CE.
二�����、如圖���,等腰Rt△ABC中�,AB=AC���,∠BAC=90°�,D為AC上的任意一點(diǎn)���,AE⊥BD于點(diǎn)E��,CF⊥BD于點(diǎn)F.
(1)求證:①AE=EF�;②EF+CF=BE�;
2、
(2)如圖�����,若D為AC延長(zhǎng)線(或反向延長(zhǎng)線)上的任意一點(diǎn),其它條件不變�,線段EF、CF與線段BE是否存在某種確定的數(shù)量關(guān)系�?寫(xiě)出你的結(jié)論并證明;
三����、 如圖�����,△ABC�����,分別以AB��、AC為腰向形外作兩個(gè)等腰直角△ABE�����、△ACF�,過(guò)A作直線,直線分別交BC��、EF于N、M兩點(diǎn).
(1)當(dāng)直線⊥BC時(shí)�,求證:ME=MF;
(2) 當(dāng)直線經(jīng)過(guò)BC的中點(diǎn)N時(shí)��,求證:⊥EF���;
(3) 如圖��,若梯形ABCD����,AD∥BC����,分別以AB、DC為腰向形外作兩個(gè)等腰直角△ABE����、△ACF,設(shè)線段AD的垂直平分線交線段EF于點(diǎn)M���,求證:ME=MF.
四�、如圖��,在等邊ΔCBN中,點(diǎn)M為BN上一點(diǎn)����,且∠CMA=60°,AN∥BC交AM于A.
(1)判斷△ACM的形狀�,并證明你的結(jié)論;
(2)試問(wèn):線段AN+MN與CN是否存在某種確定的數(shù)量關(guān)系�?試證明你的猜想;
(3)若點(diǎn)M為BN的延長(zhǎng)線上任一點(diǎn)(不包括N點(diǎn))��,(1)���、(2)②中的結(jié)論還成立嗎?請(qǐng)畫(huà)出圖形�,并證明你的猜想.
3
 2018年七年級(jí)升八年級(jí)數(shù)學(xué) 暑期銜接班講義 第二十講 專(zhuān)題七 綜合題題型專(zhuān)題訓(xùn)練(無(wú)答案) 新人教版
2018年七年級(jí)升八年級(jí)數(shù)學(xué) 暑期銜接班講義 第二十講 專(zhuān)題七 綜合題題型專(zhuān)題訓(xùn)練(無(wú)答案) 新人教版