2022年高一上學(xué)期期末考試數(shù)學(xué)試題 缺答案(I)

《2022年高一上學(xué)期期末考試數(shù)學(xué)試題 缺答案(I)》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高一上學(xué)期期末考試數(shù)學(xué)試題 缺答案(I)（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

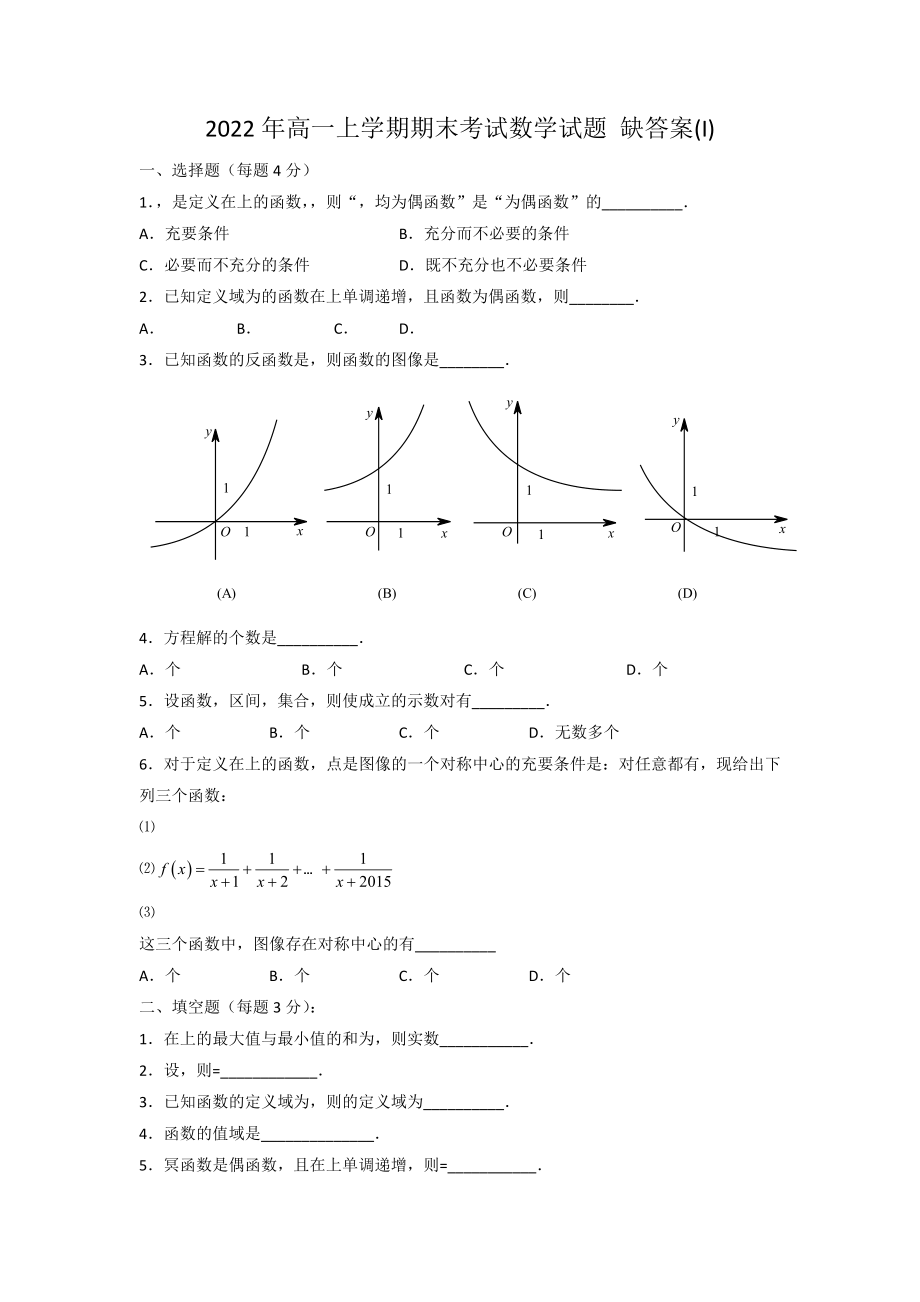
1、2022年高一上學(xué)期期末考試數(shù)學(xué)試題 缺答案(I) 一、選擇題（每題4分） 1．，是定義在上的函數(shù)，，則“，均為偶函數(shù)”是“為偶函數(shù)”的__________． A．充要條件 B．充分而不必要的條件 C．必要而不充分的條件 D．既不充分也不必要條件 2．已知定義域?yàn)榈暮瘮?shù)在上單調(diào)遞增，且函數(shù)為偶函數(shù)，則________． A． B． C． D． 3．已知函數(shù)的反函數(shù)是，則函數(shù)的圖像是________． 4．方程解的個(gè)數(shù)是__________． A．個(gè) B．個(gè) C．個(gè) D．個(gè) 5．設(shè)函數(shù)，區(qū)間，集合，則使成立的示數(shù)對(duì)有_______

2、__． A．個(gè) B．個(gè) C．個(gè) D．無數(shù)多個(gè) 6．對(duì)于定義在上的函數(shù)，點(diǎn)是圖像的一個(gè)對(duì)稱中心的充要條件是：對(duì)任意都有，現(xiàn)給出下列三個(gè)函數(shù)： ⑴ ⑵ ⑶ 這三個(gè)函數(shù)中，圖像存在對(duì)稱中心的有__________ A．個(gè) B．個(gè) C．個(gè) D．個(gè) 二、填空題（每題3分）： 1．在上的最大值與最小值的和為，則實(shí)數(shù)___________． 2．設(shè)，則=____________． 3．已知函數(shù)的定義域?yàn)?，則的定義域?yàn)開_________． 4．函數(shù)的值域是______________． 5．冥函數(shù)是偶函數(shù)，且在上單調(diào)遞增，則=___________． 6．

3、設(shè)的反函數(shù)為，若，則______． 7．函數(shù)的值域是____________． 8．已知函數(shù)，若存在，，，使成立，則實(shí)數(shù)的取值范圍是__________． 9．函數(shù)的單調(diào)遞增區(qū)間是_________________． 10．已知在上單調(diào)遞增，則實(shí)數(shù)的取值范圍是________． 11．【幕古開明】已知，，集合，且函數(shù)是偶函數(shù)，則的取值范圍是_________． 12．【雌雄莫辯】若實(shí)數(shù)滿足，稱為函數(shù)的不動(dòng)點(diǎn)．有下面三個(gè)命題： ⑴若是二次函數(shù)，且沒有不動(dòng)點(diǎn)，則函數(shù)也沒有不動(dòng)點(diǎn)； ⑵若是二次函數(shù)，則函數(shù)可能有個(gè)不動(dòng)點(diǎn)； ⑶若的不動(dòng)點(diǎn)的個(gè)數(shù)是，則的不動(dòng)點(diǎn)的個(gè)數(shù)不可能是． 它們中所

4、有真命題的序號(hào)是________________________． 三、解答題（8+6+8+8+10）： 1．求下列函數(shù)的反函數(shù)： ⑴ ⑵ 2．⑴解方程： ⑵解不等式： 3．在某次下考古活動(dòng)中，需要潛水員潛入水深為米的水底進(jìn)行作業(yè)．其用氧量包含個(gè)方面：①下潛時(shí)，平均速度為（米/單位時(shí)間），單位時(shí)間內(nèi)用氧量為（為正常數(shù)）；②在水底作業(yè)需個(gè)單位時(shí)間，每個(gè)單位時(shí)間用氧量為；③返回水面時(shí)，平均速度為（米/單位時(shí)間），單位時(shí)間用氧量為．記該潛水員在此考古活動(dòng)中，總用氧量為． ⑴將表示為的函數(shù)； ⑵設(shè)，試確定下潛速度，使總的用氧量最少． 4．寫出函數(shù)的定義域，判斷并證明其奇偶性和單調(diào)性，并求出其所有零點(diǎn)和值域． 5．對(duì)定義在上的函數(shù)和常數(shù)，，若恒成立，則稱為函數(shù)的一個(gè)“凱森數(shù)對(duì)”． ⑴若是的一個(gè)“凱森數(shù)對(duì)”，且，求； ⑵已知函數(shù)與的定義域都為，問它們是否存在“凱森數(shù)對(duì)”？分別給出判斷并說明理由； ⑶若是的一個(gè)“凱森數(shù)對(duì)”，且當(dāng)時(shí)，，求在區(qū)間上的不動(dòng)點(diǎn)個(gè)數(shù)（不動(dòng)點(diǎn)的概念參考填空題第12題）