《2022年高中數(shù)學(xué) 簡(jiǎn)單的線性規(guī)劃的應(yīng)用學(xué)生版 北師大必修5》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高中數(shù)學(xué) 簡(jiǎn)單的線性規(guī)劃的應(yīng)用學(xué)生版 北師大必修5（2頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、2022年高中數(shù)學(xué) 簡(jiǎn)單的線性規(guī)劃的應(yīng)用學(xué)生版 北師大必修5
第三章第節(jié)
課題名稱
簡(jiǎn)單線性規(guī)劃的應(yīng)用
授課時(shí)間
第 周星期 第 節(jié)
課型
新授課
主備課人
衛(wèi)娟蓮
學(xué)習(xí)目標(biāo)
從實(shí)際情境中抽象出簡(jiǎn)單線性規(guī)劃問題并解決
重點(diǎn)難點(diǎn)
列出約束條件及寫出目標(biāo)函數(shù)
學(xué)習(xí)過程
與方法
1. 自主學(xué)習(xí)：
若實(shí)數(shù)滿足求的最大值及最小值
2.精講互動(dòng)：
例1：某工廠生產(chǎn)甲、乙兩種產(chǎn)品.已知生產(chǎn)甲種產(chǎn)品1t需消耗A種礦石10t、B種礦石5t、煤4t；生產(chǎn)乙種產(chǎn)品1噸需消耗A種礦石4t、B種礦石4t、煤9t.每1t甲種產(chǎn)品的利潤是600元,每1t乙種產(chǎn)品的利潤是1
2、000元.工廠在生產(chǎn)這兩種產(chǎn)品的計(jì)劃中要求消耗A種礦石不超過300t、消耗B種礦石不超過200t、消耗煤不超過360t.甲、乙兩種產(chǎn)品應(yīng)各生產(chǎn)多少(精確到0.1t),能使利潤總額達(dá)到最大?
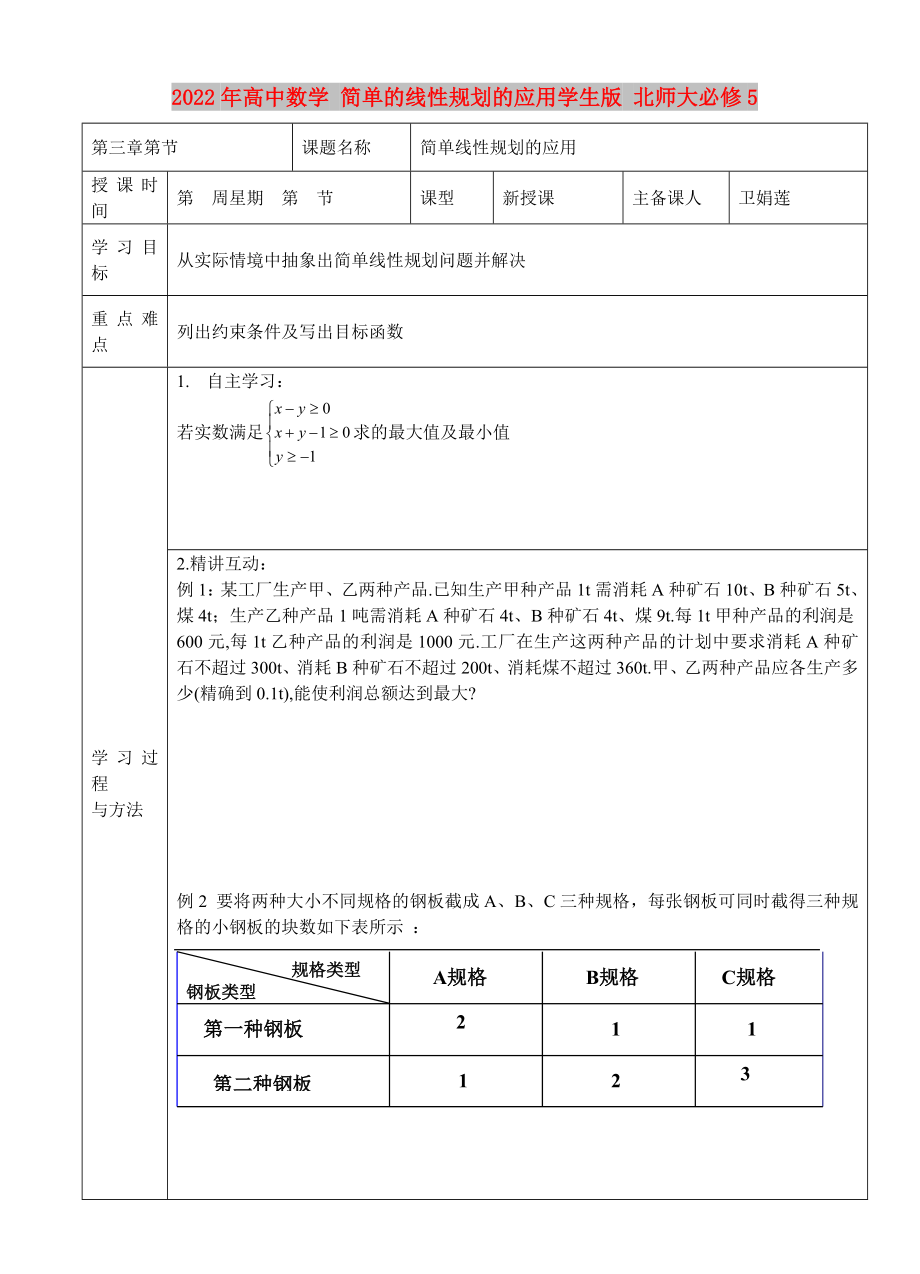
例2 要將兩種大小不同規(guī)格的鋼板截成A、B、C三種規(guī)格，每張鋼板可同時(shí)截得三種規(guī)格的小鋼板的塊數(shù)如下表所示 ：
規(guī)格類型
鋼板類型
第一種鋼板
A規(guī)格
B規(guī)格
C規(guī)格
2
1
2
1
3
1
第二種鋼板
在可行域內(nèi)找出最優(yōu)解、線性規(guī)劃整數(shù)解問題的一般方法是：
1.若區(qū)域“頂點(diǎn)”處恰好為整點(diǎn)，那么它就是最優(yōu)解；（在包括邊
3、界的情況下）
2.若區(qū)域“頂點(diǎn)”不是整點(diǎn)或不包括邊界時(shí)，應(yīng)先求出該點(diǎn)坐標(biāo)，并計(jì)算目標(biāo)函數(shù)值Z，然后在可行域內(nèi)適當(dāng)放縮目標(biāo)函數(shù)值，使它為整數(shù)，且與Z最接近，在這條對(duì)應(yīng)的直線中，取可行域內(nèi)整點(diǎn)，如果沒有整點(diǎn)，繼續(xù)放縮，直至取到整點(diǎn)為止。
3.在可行域內(nèi)找整數(shù)解，一般采用平移找解法，即打網(wǎng)絡(luò)、找整點(diǎn)、平移直線、找出整數(shù)最優(yōu)解
3達(dá)標(biāo)訓(xùn)練：
①咖啡館配制兩種飲料．甲種飲料每杯含奶粉9g 、咖啡4g、糖3g,乙種飲料每杯含奶粉4g 、咖啡5g、糖10g．已知每天原料的使用限額為奶粉3600g ，咖啡xxg 糖3000g,如果甲種飲料每杯能獲利0.7元，乙種飲料每杯能獲利1.2元，每天在原料的
4、使用限額內(nèi)飲料能全部售出，每天應(yīng)配制兩種飲料各多少杯能獲利最大？
②某家具廠有方木材90m3，木工板600m3，準(zhǔn)備加工成書桌和書櫥出售，已知生產(chǎn)每張書桌需要方木料0.1m3、木工板2m3；生產(chǎn)每個(gè)書櫥需要方木料0.2m3，木工板1m3，出售一張書桌可以獲利80元，出售一張書櫥可以獲利120元（1）怎樣安排生產(chǎn)可以獲利最大？（2）若只生產(chǎn)書桌可以獲利多少？（3）若只生產(chǎn)書櫥可以獲利多少？
課堂小結(jié)
解線性規(guī)劃應(yīng)用問題的一般步驟：1）理清題意，列出表格：2）設(shè)好變?cè)⒘谐霾坏仁浇M和目標(biāo)函數(shù)3）由二元一次不等式表示的平面區(qū)域做出可行域；4）在可行域內(nèi)求目標(biāo)函數(shù)的最優(yōu)解5)還原成實(shí)際問題（準(zhǔn)確作圖，準(zhǔn)確計(jì)算)
作業(yè)布置
課后反思
審核
備課組（教研組）： 教務(wù)處：
2022年高中數(shù)學(xué) 簡(jiǎn)單的線性規(guī)劃的應(yīng)用學(xué)生版 北師大必修5
