《2022年高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識 第一章 第一節(jié)集合的概念與運算 理》由會員分享�����,可在線閱讀����,更多相關(guān)《2022年高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識 第一章 第一節(jié)集合的概念與運算 理(6頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1��、2022年高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識 第一章 第一節(jié)集合的概念與運算 理
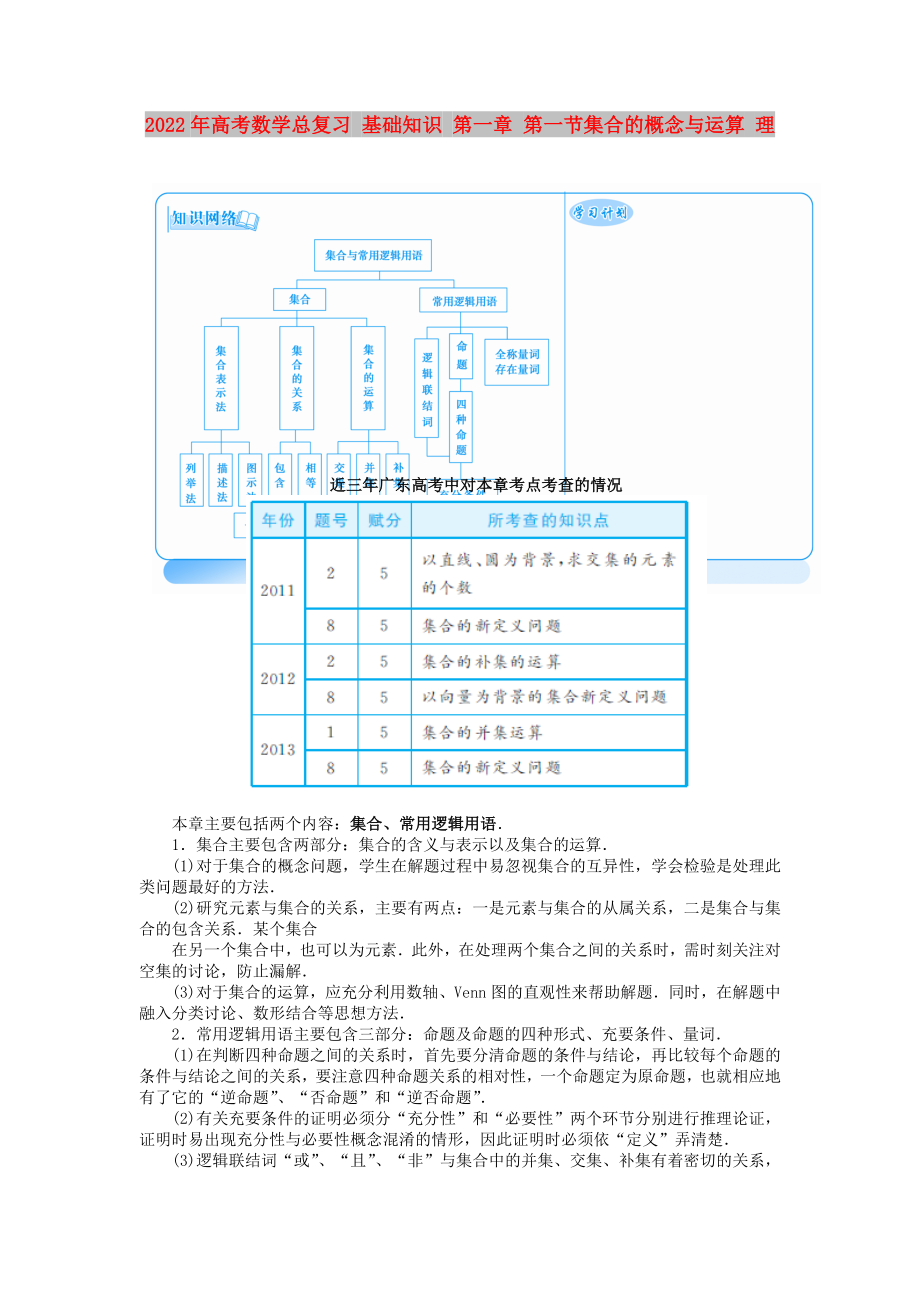
近三年廣東高考中對本章考點考查的情況
本章主要包括兩個內(nèi)容:集合����、常用邏輯用語.
1.集合主要包含兩部分:集合的含義與表示以及集合的運算.
(1)對于集合的概念問題�����,學(xué)生在解題過程中易忽視集合的互異性,學(xué)會檢驗是處理此類問題最好的方法.
(2)研究元素與集合的關(guān)系��,主要有兩點:一是元素與集合的從屬關(guān)系�,二是集合與集合的包含關(guān)系.某個集合
在另一個集合中,也可以為元素.此外���,在處理兩個集合之間的關(guān)系時��,需時刻關(guān)注對空集的討論���,防止漏解.
(
2、3)對于集合的運算�,應(yīng)充分利用數(shù)軸、Venn圖的直觀性來幫助解題.同時�����,在解題中融入分類討論���、數(shù)形結(jié)合等思想方法.
2.常用邏輯用語主要包含三部分:命題及命題的四種形式�、充要條件�、量詞.
(1)在判斷四種命題之間的關(guān)系時�,首先要分清命題的條件與結(jié)論���,再比較每個命題的條件與結(jié)論之間的關(guān)系����,要注意四種命題關(guān)系的相對性��,一個命題定為原命題���,也就相應(yīng)地有了它的“逆命題”��、“否命題”和“逆否命題”.
(2)有關(guān)充要條件的證明必須分“充分性”和“必要性”兩個環(huán)節(jié)分別進(jìn)行推理論證�,證明時易出現(xiàn)充分性與必要性概念混淆的情形�����,因此證明時必須依“定義”弄清楚.
(3)邏輯聯(lián)結(jié)詞“或”����、“且”、“非”與集合
3����、中的并集、交集�、補(bǔ)集有著密切的關(guān)系,要注意類比.其中對邏輯聯(lián)結(jié)詞“或”的理解是難點.
(4)全(特)稱命題的否定與命題的否定有區(qū)別����,全(特)稱命題的否定是將其全稱量詞改為存在量詞(或存在量詞改為全稱量詞),并把結(jié)論否定���,而命題的否定則是直接否定結(jié)論即可. 從近幾年的高考題來看���,常以邏輯聯(lián)結(jié)詞“或”、“且”���、“非”為工具�����,考查函數(shù)�、不等式�����、數(shù)列�、立體幾何��、解析幾何等知識.
預(yù)測高考仍以選擇題�、填空題為主要考查題型�,難度以容易題為主,以基本概念����、基本方法為考查對象,以函數(shù)��、不等式��、三角����、立體幾何、解析幾何等知識為依托����,重點考查集合的運算,全稱命題與特稱命題的否定��,判斷特稱命題�����、全稱命題的真假
4、���,確定充分(或必要)條件等內(nèi)容.
本章內(nèi)容概念性強(qiáng),考題大都為容易的選擇題�����,因此復(fù)習(xí)中應(yīng)注意:
1.復(fù)習(xí)集合��,可以從兩個方面入手��,一方面是集合的概念之間的區(qū)別與聯(lián)系����,另一方面是對集合知識的應(yīng)用.
2.主要是把握集合與元素、集合與集合之間的關(guān)系����,弄清有關(guān)的術(shù)語和符號,特別是對集合中的元素的屬性要分清楚.
3.要注意邏輯聯(lián)結(jié)詞“或”����、“且”、“非”與集合中的“并”����、“交”�����、“補(bǔ)”是相關(guān)的���,二者相互對照可加深對雙方的認(rèn)識和理解.
4.復(fù)習(xí)常用邏輯用語知識時,要抓住所學(xué)的幾個知識點��,通過解決一些簡單的問題達(dá)到理解����、掌握常用邏輯知識的目的.
要突出常用邏輯用語的工具性作用,從概念入
5�、手,根據(jù)有關(guān)的符號���、術(shù)語��、關(guān)系�����、條件�����,結(jié)合實際問題進(jìn)行邏輯推理��,重點是命題的相互關(guān)系���,全稱量詞、存在量詞及其否定����,確定命題成立的充分或必要條件.復(fù)習(xí)應(yīng)側(cè)重于以下幾點:
(1)能寫出已知命題的四種形式,會根據(jù)命題的相互關(guān)系判斷充分(或必要)條件�����、充要條件.
(2)了解簡單邏輯聯(lián)結(jié)詞�����,能用數(shù)學(xué)符號表示命題����,并能根據(jù)簡單命題的真假判定復(fù)合命題的真假.
(3)理解全稱量詞、存在量詞及其關(guān)系,能區(qū)分否命題與命題的否定的不同.
5.集合多與函數(shù)����、方程、不等式有關(guān)�����,要注意知識的融會貫通.
第一節(jié) 集合的概念與運算
1.集合的含義與表示:
(1)了解集合的含義����、元
6、素與集合的屬于關(guān)系.
(2)能用自然語言���、圖形語言����、集合語言(列舉法或描述法)描述不同的具體問題.
2.集合間的基本關(guān)系:
(1)理解集合之間包含與相等的含義�,能識別給定集合的子集.
(2)在具體情境中了解全集與空集的含義.
3.集合的基本運算:
(1)理解兩個集合的并集與交集的含義,會求兩個簡單集合的并集與交集.
(2)理解在給定集合中一個子集的補(bǔ)集的含義��,會求給定子集的補(bǔ)集.
(3)能使用韋恩(Venn)圖表達(dá)集合的關(guān)系及運算.
知識梳理
一�、集合的含義與表示方法
1.集合的含義:把研究的對象統(tǒng)稱為
7、________�,把一些元素組成的總體叫做________.
2.集合元素的性質(zhì):________�����、________�、________.
3.元素與集合的關(guān)系:①屬于��,記為________���;②不屬于��,記為________.
4.集合的表示方法:________��、________和________.
5.常用數(shù)集的記號:空集________,正整數(shù)集________��,自然數(shù)集________��、整數(shù)集________�����,有理數(shù)集________���,實數(shù)集________��,復(fù)數(shù)集________.
二��、集合間的基本關(guān)系
三�����、集合的基本運算
四�、有限集的子集數(shù)的求法
8、
設(shè)有限集A的元素個數(shù)為n���,則(1)A的子集個數(shù)為2n���;(2)A的真子集個數(shù)為2n-1;(3)A的非空子集個數(shù)為______��;(4)A的非空真子集個數(shù)為______.
基礎(chǔ)自測
1.(xx·廣州模擬)設(shè)全集U={-2��,-1,0,1,2}�,集合A={1,2},B={-2,1,2}�,則A∪(?UB)等于 ( )
A.? B.{1}
C.{1,2} D.{-1,0,1,2}
解析:由題意可知?UB={-1,0},所以A∪(?UB)={-1,0,1,2}�����,故選D.
答案:D
2.(
9、xx·北京東城區(qū)模擬)設(shè)全集U=R�,A={x|-x2-3x>0},B={x|x < -1}�����,則圖中陰影部分表示的集合為( )
A.{x|x>0}
B.{x|-3
10、A=[0�,+∞),故?UA=(-∞��,0)��,故選B.
答案:B
4.已知集合A={x|1≤x≤2}�����,B={x||x-a|≤1}�����,若A∩B=A����,則實數(shù)a的取值范圍為________.
解析:化簡得B={x|a-1≤x≤1+a}.∵A∩B=A,
∴A?B.∴a-1≤1且1+a≥2.解得1≤a≤2.
答案:[1,2]
1.(xx·廣東卷)設(shè)集合M={x|x2+2x=0���,x∈R}���,N={x|x2-2x=0�,x∈R} ����,則M∪N= ( )
A.{0} B.{0,2}
C.{-2,0} D.{
11、-2,0,2}
解析:易得M={-2,0}��,N={0,2}�����,所以M∪N={-2,0,2}��,故選D.
答案:D
2.(xx·上海卷)設(shè)常數(shù)a∈R��,集合A={x|(x-1)(x-a)≥0}���,B={x|x≥a-1}�,若A∪B=R�����,則a的取值范圍為( )
A.(-∞�,2) B.(-∞,2]
C.(2�,+∞) D.[2,+∞)
解析:集合A討論后利用數(shù)軸可知��,或
解得a≤2 �����,故選B.
答案:B
1.(xx·梅州二模)已知集合A={3��,a2}��,集合B={0��,b,1-a}����,且A∩B={1},則A∪B=( )
A.{0,1,3} B.{1
12����、,2,4}
C.{0,1,2,3} D.{0,1,2,3,4}
解析:因為集合A={3,a2}��,集合B={0,b,1-a}����,且A∩B={1},所以a2=1����,解得:a=1或a =-1,
當(dāng)a =1時����,1-a =1-1=0,不合題意��,舍去����;
當(dāng)a =-1時,1-a =1-(-1)=2�,此時b=1,
所以集合A={3,1}��,集合B={0,1,2}��,則A∪B={0,1,2,3}.故選C.
答案:C
2.(xx·廣州模擬)對于集合M����,N,定義M-N={x|x∈M����,且x?N},M⊕N=(M-N)∪(N-M)���,設(shè)A=����,B={x|x<0}����,則A⊕B=( )
A. B.
C.∪[0,+∞) D.∪(0����,+∞)
解析:因為A-B={x|x≥0},B-A=��,所以AB=.
答案:C
 2022年高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識 第一章 第一節(jié)集合的概念與運算 理
2022年高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識 第一章 第一節(jié)集合的概念與運算 理