高考數(shù)學(xué)一輪總復(fù)習(xí)（基礎(chǔ)達(dá)標(biāo)+提優(yōu)演練）第6章 第3節(jié) 二元一次不等式（組）與簡單的線性規(guī)劃 文

《高考數(shù)學(xué)一輪總復(fù)習(xí)（基礎(chǔ)達(dá)標(biāo)+提優(yōu)演練）第6章 第3節(jié) 二元一次不等式（組）與簡單的線性規(guī)劃 文》由會員分享，可在線閱讀，更多相關(guān)《高考數(shù)學(xué)一輪總復(fù)習(xí)（基礎(chǔ)達(dá)標(biāo)+提優(yōu)演練）第6章 第3節(jié) 二元一次不等式（組）與簡單的線性規(guī)劃 文（10頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

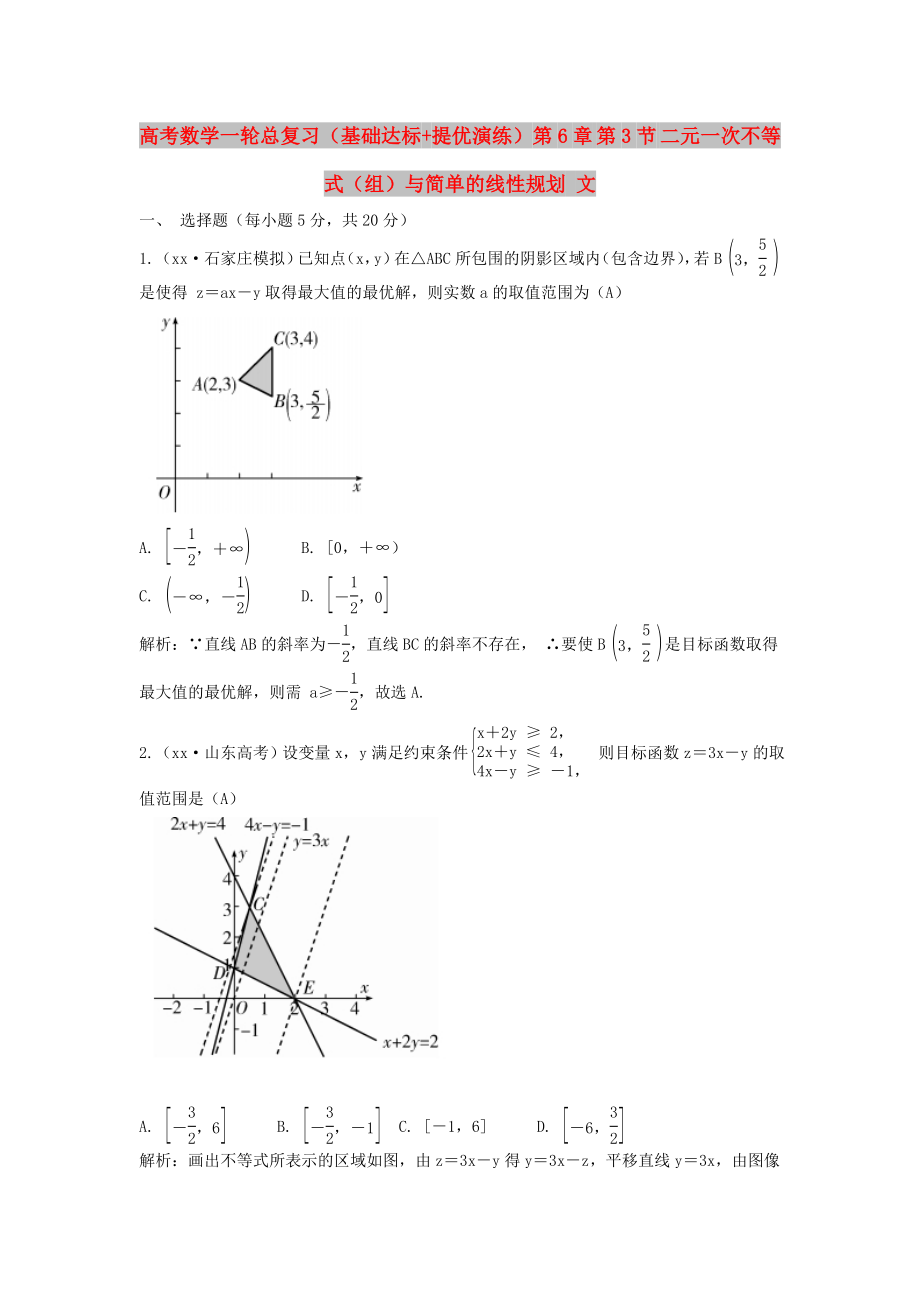
1、高考數(shù)學(xué)一輪總復(fù)習(xí)（基礎(chǔ)達(dá)標(biāo)+提優(yōu)演練）第6章 第3節(jié) 二元一次不等式（組）與簡單的線性規(guī)劃 文 一、 選擇題（每小題5分，共20分） 1.（xx·石家莊模擬）已知點(diǎn)（x，y）在△ABC所包圍的陰影區(qū)域內(nèi)（包含邊界），若B是使得 z＝ax－y取得最大值的最優(yōu)解，則實(shí)數(shù)a的取值范圍為（A） A. 　　 B. [0，＋∞）　　 C. 　　 D. 解析：∵直線AB的斜率為－，直線BC的斜率不存在， ∴要使B是目標(biāo)函數(shù)取得最大值的最優(yōu)解，則需 a≥－，故選A. 2.（xx·山東高考）設(shè)變量x，y滿足約束條件 則目標(biāo)函數(shù)z＝3x－y的取值范圍是（A） A. 　　 B

2、. C. [－1，6]　　 D. 解析：畫出不等式所表示的區(qū)域如圖，由z＝3x－y得y＝3x－z，平移直線y＝3x，由圖像可知當(dāng)直線經(jīng)過點(diǎn)E（2，0）時，直線y＝3x－z的截距最小，此時z最大為z＝3x－y＝6，當(dāng)直線經(jīng)過C點(diǎn)時，直線截距最大，此時z最小，由解得此時z＝3x－y＝－3＝－，∴z＝3x－y的取值范圍是，選A. 3. （xx·淮南模擬）若實(shí)數(shù)x，y滿足不等式組則該不等式組表示的平面區(qū)域的面積是（C） A. 3　　 B. 　　 C. 2　　 D. 2 解析：不等式組 表示的平面區(qū)域如圖所示（陰影部分），易知△ABC為直角三角形，且A（0，1），B（2，3）， C

3、（1，0），則面積為S＝×2×＝2 . 4. （xx·湖南十校聯(lián)考）設(shè)變量x，y滿足約束條件則目標(biāo)函數(shù)z＝2x＋3y＋1的最大值為（B） A. 11　　 B. 10　　 C. 9　　 D. 8.5 解析：由約束條件可畫出可行域，平移參照直線2x＋3y＋1＝0可知，在可行域的頂點(diǎn)（3，1）處，目標(biāo)函數(shù)z＝2x＋3y＋1取得最大值，zmax＝2×3＋3×1＋1＝10。 二、 填空題（每小題5分，共10分） 5.（xx·昆明調(diào)研）已知變量x，y滿足條件則2x－y的最大值為　?。? 解析：在坐標(biāo)平面內(nèi)畫出題中的不等式組表示的平面區(qū)域及直線2x－y＝0，平移該直線，當(dāng)平移

4、到經(jīng)過該平面區(qū)域內(nèi)的點(diǎn)時，此時2x－y取得最大值，最大值是2x－y＝2×－＝. 6. （xx·廣東高考）給定區(qū)域D：令點(diǎn)集T＝{（x0，y0）∈D|x0，y0∈Z，（x0，y0）是z＝x＋y在D上取得最大值或最小值的點(diǎn)}，則T中的點(diǎn)共確定　6　條不同的直線. 解析： 解決本題的關(guān)鍵是要讀懂?dāng)?shù)學(xué)語言，x0，y0∈Z，說明x0，y0是整數(shù)，作出圖形可知，△ABF所圍成的區(qū)域即為區(qū)域D，其中A（0，1）是z在D上取得最小值的點(diǎn)，B，C，D，E，F(xiàn)，是z在D上取得最大值的點(diǎn)，則T中的點(diǎn)共確定AB，AC，AD，AE，AF，BF共6條不同的直線. 三、 解答題（共20分） 7. （10分

5、）某工廠生產(chǎn)甲、乙兩種產(chǎn)品，需要經(jīng)過金Ⅰ和裝配兩個車間加工，有關(guān)數(shù)據(jù)如下表： 列出滿足生產(chǎn)條件的數(shù)學(xué)關(guān)系式，并畫出相應(yīng)的平面區(qū)域. 解析： 設(shè)共生產(chǎn)甲、乙兩種產(chǎn)品各x件和y件， 于是x，y滿足約束條件：（6分） 在直角坐標(biāo)系中作出不等式組表示的平面區(qū)域，如圖陰影部分所示. （10分） 8. （10分）某企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品，已知生產(chǎn)每噸甲產(chǎn)品要用A原料3噸、B原料2噸；生產(chǎn)每噸乙產(chǎn)品要用A原料1噸、B原料3噸.銷售每噸甲產(chǎn)品可獲得利潤5萬元、銷售每噸乙產(chǎn)品可獲得利潤3萬元.該企業(yè)在一個生產(chǎn)周期內(nèi)消耗A原料不超過13噸、B原料不超過18噸，求該企業(yè)可獲得的最大利潤. 解析：

6、 設(shè)該企業(yè)在一個生產(chǎn)周期內(nèi)分別生產(chǎn)甲、乙兩種產(chǎn)品x噸、y噸，所獲得的利潤是z萬元，則依題意有且z＝5x＋3y.（4分） 在坐標(biāo)平面內(nèi)作出不等式組表示的平面區(qū)域及直線5x＋3y＝0，如圖，平移直線5x＋3y＝0，注意到當(dāng)直線平移到經(jīng)過該平面區(qū)域內(nèi)的點(diǎn)（3，4）時，相應(yīng)直線在x軸上的截距最大，此時z＝5x＋3y取得最大值，最大值是27.（9分） ∴該企業(yè)可獲得的最大利潤為27萬元.（10分） （時間：30分鐘　滿分：50分） 若時間有限，建議選講2，4，8 一、 選擇題（每小題5分，共20分） 1,。 （xx·全國高考）已知正三角形ABC的頂點(diǎn)A（1，1），B（1，3），頂點(diǎn)C在第

7、一象限，若點(diǎn)（x，y）在△ABC內(nèi)部，則 z＝－x＋y的取值范圍是（A） A. （1－，2）　　 B. （0，2）　　 C. （－1，2）　　 D. （0，1＋） 解析：作出三角形區(qū)域如圖，由圖像可知當(dāng)直線y＝x＋z經(jīng)過點(diǎn)B時，截距最大，此時z＝－1＋3＝2，當(dāng)直線經(jīng)過點(diǎn)C時，直線截距最小.∵AB⊥x軸，∴yC＝＝2，三角形的邊長為2，設(shè)C（x，2），則AC＝＝2，解得（x－1）2＝3，x＝1±，∵頂點(diǎn)C在第一象限，∴x＝1＋，即（1＋，2）代入直線z＝－x＋y得z＝－（1＋）＋2＝1－，∴z的取值范圍是（1－，2），故選A. 2. 在坐標(biāo)平面內(nèi)，不等式組所表示的平面區(qū)域

8、的面積為（B） A. 2　　 B. 　　 C. 　　 D. 2 解析： 不等式組表示的平面區(qū)域?yàn)槿鐖D所示的陰影部分，又y＝x＋1，y＝2x－1的交點(diǎn)B的橫坐標(biāo)為2，由y＝－2x－1， y＝x＋1解得點(diǎn)C的橫坐標(biāo)為－，∴S△ABC＝·AD·（|xC|＋|xB|）＝×2×＝. 3． （xx·山東高考）在平面直角坐標(biāo)系xOy中，M為不等式組：所表示的區(qū)域上一動點(diǎn)，則直線OM斜率的最小值為（C） A. 2　　 B. 1　　 C. －　　 D. － 解析： 不等式組所表示的區(qū)域如圖所示，當(dāng)點(diǎn)M在直線x＋2y－1＝0與直線3x＋y－8＝0的交點(diǎn)（3，－1）處時，斜率有最小值

9、－.故選C. 4. （xx·鄭州質(zhì)檢）設(shè)f（x）是定義在R上的增函數(shù)，且對于任意的x都有f（2－x）＋f（x）＝0恒成立，如果實(shí)數(shù)m，n滿足不等式組則m2＋n2的取值范圍是（C） A. （3，7）　　 B. （9，25）　　 C. （13，49）　　 D. （9，49） 解析： 依題意得－f（n2－8n）＝f（2－n2＋8n），于是題中的不等式組等價于又函數(shù)f（x）是R上的增函數(shù)，∴不等式組等價于即注意到m2＋n2＝（）2可視為動點(diǎn)（m，n）與原點(diǎn)的距離的平方，因此問題可轉(zhuǎn)化為不等式組表示的平面區(qū)域內(nèi)的所有的點(diǎn)（m，n）與原點(diǎn)的距離的平方的取值范圍，該不等式組表示的平面區(qū)域

10、是如圖所示的半圓及直線m＝3所圍成的區(qū)域（不含邊界）.結(jié)合圖像不難得知，平面區(qū)域內(nèi)的所有的點(diǎn)與原點(diǎn)的距離的平方應(yīng)大于原點(diǎn)與點(diǎn)（3，2）的距離的平方，應(yīng)小于原點(diǎn)與點(diǎn)（3，4）的距離再加上2的和的平方，即當(dāng)m>3時，m2＋n2的取值范圍是（13，49），故選C. 二、 填空題（每小題5分，共10分） 5. （xx·江南十校聯(lián)考）設(shè)動點(diǎn)P（x，y）在區(qū)域Ω： 上（含邊界），過點(diǎn)P任意作直線l，設(shè)直線l與區(qū)域Ω的公共部分為線段AB，則以AB為直徑的圓的面積的最大值為　4π　. 解析： 如圖，區(qū)域Ω為△MON及其內(nèi)部，由于線段AB為直線l與區(qū)域Ω的公共部分，則|AB|的最大值為|OM|＝4

11、. ∴以AB為直徑的圓的面積的最大值為π·＝4π. 6.（xx·江西七校聯(lián)考）已知實(shí)數(shù)x，y滿足若是使ax－y取得最小值的唯一的可行解，則實(shí)數(shù)a的取值范圍為　?。? 解析： 記z＝ax－y，注意到當(dāng)x＝0時，y＝－z，即直線 z＝ax－y在y軸上的截距是－z.在坐標(biāo)平面內(nèi)畫出題中的不等式組表示的平面區(qū)域，如圖所示，結(jié)合圖形可知，滿足題意的實(shí)數(shù)a的取值范圍為. 三、 解答題（共20分） 7. （10分）（xx·廣東聯(lián)考）2012年9月19日《汕頭日報(bào)》報(bào)道：汕頭市西部生態(tài)新城啟動建設(shè)，由金平區(qū)招商引資共30億元建設(shè)若干個項(xiàng)目.現(xiàn)有某投資人打算投資甲、乙兩個項(xiàng)目，根據(jù)預(yù)測，

12、甲、乙項(xiàng)目可能的最大盈利率分別為100%和50%，可能的最大虧損率分別為30%和10%.該投資人計(jì)劃投資金額不超過10億元，為確保可能的資金虧損不超過1.8億元，問：該投資人對甲、乙兩個項(xiàng)目各投資多少億元，才能使可能的盈利最大？ 解析： 設(shè)該投資人對甲、乙兩個項(xiàng)目分別投資x億元、y億元，可能的盈利為z億元，則z＝x＋y . 依題意得即（3分） 作出可行域如圖陰影部分所示， 作出直線l0：x＋y＝0. 作l0的一組平行線l：y＝－2x＋2z， 當(dāng)直線過直線x＋y－10＝0與直線3x＋y－18＝0的交點(diǎn)A時直線在 y軸上的截距2z最大，此時z最大，（6分） 解方程組得∴A（4

13、，6）， ∴zmax＝4＋×6＝7.（9分） 故投資人對甲項(xiàng)目投資4億元、對乙項(xiàng)目投資6億元，才能使可能的盈利最大.（10分） 8. （10分）甲、乙兩公司生產(chǎn)同一種商品，但由于設(shè)備陳舊，需要更新.經(jīng)測算，對于函數(shù)f（x），g（x）及任意的x≥0，當(dāng)甲公司投入x萬元改造設(shè)備時，若乙公司投入改造設(shè)備費(fèi)用小于f（x）萬元，則乙有倒閉的風(fēng)險，否則無倒閉的風(fēng)險；同樣，當(dāng)乙公司投入x萬元改造設(shè)備時，若甲公司投入改造設(shè)備費(fèi)用小于g（x）萬元，則甲有倒閉的風(fēng)險，否則無倒閉的風(fēng)險. （1）請解釋f（0），g（0）的實(shí)際意義； （2）設(shè)f（x）＝x＋5，g（x）＝x＋10，甲、乙兩公司為了避免惡性競爭

14、，經(jīng)過協(xié)商同意在雙方均無倒閉風(fēng)險的情況下盡可能減少改造設(shè)備資金.問此時甲、乙兩公司各投入多少萬元？ 解析： （1）f（0）表示當(dāng)甲不投入資金改造設(shè)備，乙要避免倒閉，至少要投入f（0）萬元的資金；（2分） g（0）表示當(dāng)乙不投入資金改造設(shè)備，甲要避免倒閉，至少要投入 g（0）萬元的資金.（4分） （2）設(shè)甲公司投入的資金為x萬元，乙公司投入的資金為 y萬元，兩公司的總投入為z萬元. 由題意，甲、乙兩公司均無倒閉風(fēng)險，需 即　 （7分） 目標(biāo)函數(shù)為z＝x＋y.不等式組所表示的平面區(qū)域如圖所示. 由圖可知當(dāng)經(jīng)過點(diǎn)A時，兩公司投入資金最少. 由得故A（25，30）.（9分） 故在雙方均無倒閉風(fēng)險的情況下，甲公司至少投入25萬元，乙公司至少投入30萬元.（10分）