《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 向量的加法教案 北師大版必修4(通用)》由會(huì)員分享��,可在線閱讀���,更多相關(guān)《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 向量的加法教案 北師大版必修4(通用)(6頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1��、陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 向量的加法教案 北師大版必修4
一��、教學(xué)目標(biāo)
知識(shí)目標(biāo):理解向量加法的含義����,會(huì)用向量加法的三角形法則和平行四邊形法則作出兩個(gè)向量的和;
掌握向量加法的交換律與結(jié)合律��,并會(huì)用它們進(jìn)行向量運(yùn)算.
能力目標(biāo):經(jīng)歷向量加法概念����、法則的建構(gòu)過程,感受和體會(huì)將實(shí)際問題抽象為數(shù)學(xué)概念的過程和思想��,培養(yǎng)學(xué)生發(fā)現(xiàn)問題����、分析問題、解決問題的能力.
情感目標(biāo):經(jīng)歷運(yùn)用數(shù)學(xué)描述和刻畫現(xiàn)實(shí)世界的過程��,體驗(yàn)探索的樂趣�,激發(fā)學(xué)生的學(xué)習(xí)熱情.培養(yǎng)學(xué)生勇于探索、創(chuàng)新的個(gè)性品質(zhì).
二.重點(diǎn)難點(diǎn)
重點(diǎn):向量加法運(yùn)算的意義和法則.
難點(diǎn):向量加法法則的理解.
三.教學(xué)方法
采
2�����、用“啟發(fā)探究”式教學(xué)方法����,結(jié)合多媒體輔助教學(xué).
四.教學(xué)過程
Ⅰ.創(chuàng)設(shè)情境 直觀感知
A
O
B
斜拉索
塔柱
斜拉橋示意圖
梁
O
F
1
F
2
F
斜拉索
塔柱
斜拉橋示意圖
斜拉索
塔柱
斜拉橋示意圖
O
F
1
F
2
F
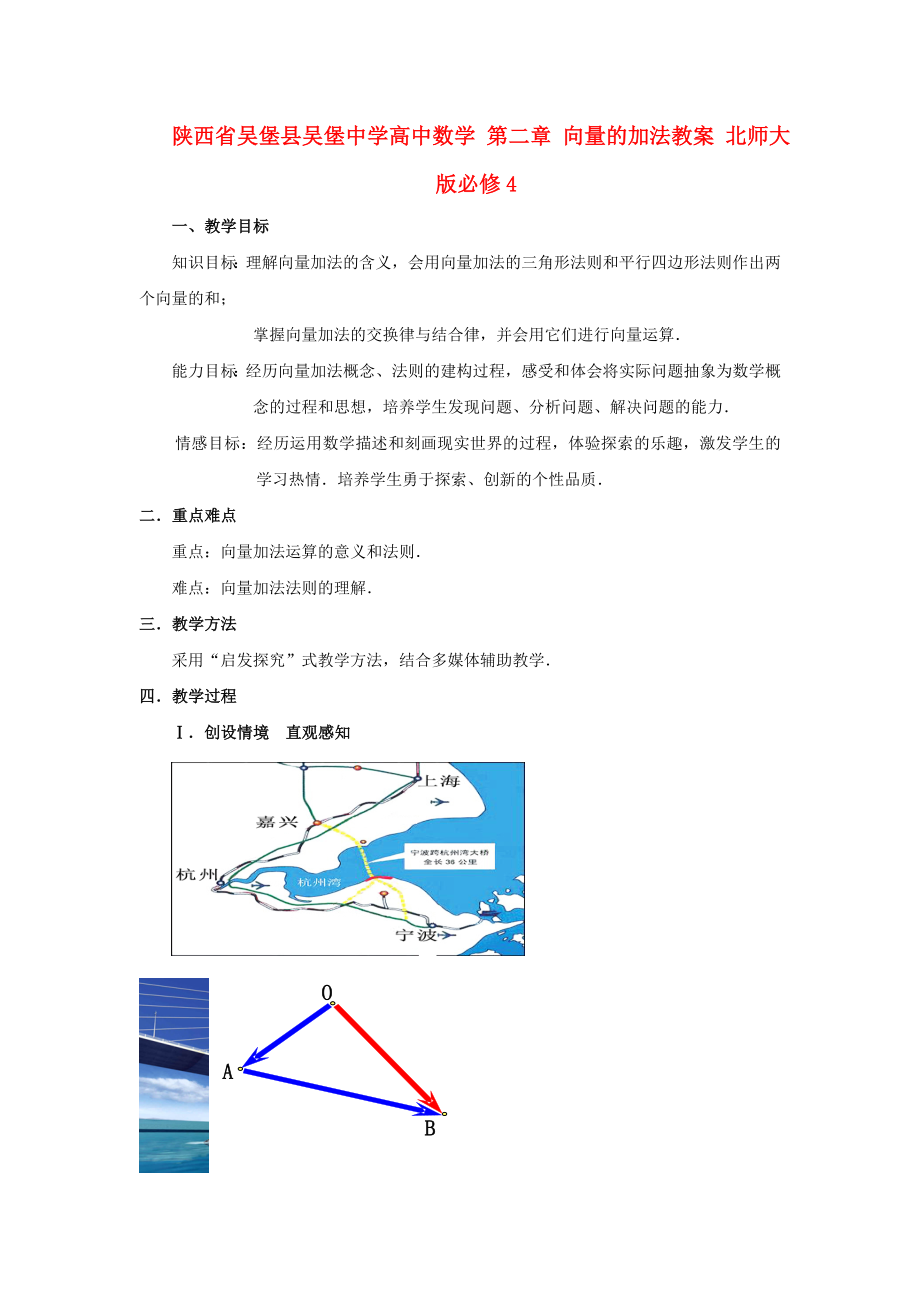
以杭州灣大橋?yàn)檎w背景,設(shè)計(jì)兩個(gè)問題情境如下:
問題1:建橋之前如何從嘉興到達(dá)寧波�����?建橋之后可以從嘉興直達(dá)寧波���,此時(shí)的位移與前面兩次位移的結(jié)果有何關(guān)系�����??jī)纱挝灰频慕Y(jié)果可稱為兩次位移的和����,如何用等式來刻畫這三個(gè)位移的關(guān)系���?
問題2:這是大橋南端的A型獨(dú)塔斜拉橋�,其中兩根拉索對(duì)塔柱的拉力分別
3����、為��、�����,則它們對(duì)塔柱的共同作用效果如何�?合力可稱為力與的和���,如何用等式來刻畫這三個(gè)力的關(guān)系���?
力與位移都是物理中的矢量,既有大小又有方向����,若去掉它們的物理屬性,就是數(shù)學(xué)中的向量.它們的和也就可以抽象成向量與向量之間的一種運(yùn)算——向量的加法(引出課題)
Ⅱ.抽象概括 形成定義
(一)建立數(shù)學(xué)模型
若記則向量叫做向量與的和���,記為 .
問題3:如圖所示的三個(gè)向量�,你們能給出它們所滿足的等式嗎���?—— ��,即向量為向量與的和
(二)抽象數(shù)學(xué)概念
問題4:由此����,你們能概括出一般的兩個(gè)向量與和的定義嗎?
學(xué)生活動(dòng):在平面內(nèi)任取一點(diǎn)O����,平移使其起點(diǎn)為點(diǎn)O����,平移使其起點(diǎn)與向量的終點(diǎn)重
4、合��,再連接向量的起點(diǎn)與向量的終點(diǎn).
(1)平移的目的是什么��?——平移后使得兩個(gè)向量能在同一個(gè)三角形中�;
(2)平移后兩個(gè)向量的終點(diǎn)與起點(diǎn)有何關(guān)系?——使得第二個(gè)向量的終點(diǎn)與第一個(gè)向量的起點(diǎn)重合����;
(3)和向量又是什么?——連接向量的起點(diǎn)與向量的終點(diǎn)���,并指向的終點(diǎn)����,得到的向量即為向量與的和;
(4)借助于幾何直觀����,用自然簡(jiǎn)潔的語言給出兩個(gè)向量和的定義 .
和的定義:已知向量,在平面內(nèi)任取一點(diǎn)O�,作,則向量叫做向量的和.記作:.即.
向量的加法的定義:求兩個(gè)向量和的運(yùn)算叫做向量的加法.
向量加法的法則:和的定義給出了求向量和的方法�����,稱為向量加法的三角形法則.
問題5:用三角形法
5�、則求向量和的過程中要注意什么?——平移兩個(gè)向量使它們首尾順次相連.
問題6:還可以用什么方法求兩個(gè)向量的和呢�����?——向量加法的平行四邊形法則.
問題7:平行四邊形法則有何特點(diǎn)�?——平移兩個(gè)向量至共起點(diǎn).
兩種方法求和的結(jié)果是一樣的,可見�����,向量加法的三角形法則與平行四邊形法則在本質(zhì)上是一致的.在具體求和時(shí)����,應(yīng)根據(jù)情況靈活地選擇.
(三)嘗試運(yùn)用法則
試一試:如圖��,已知���、,作出
a
b
a
b
b
a
a
b
向量加法的三角形法則對(duì)共線向量的求和仍然是適用的�,反映了三角形法則具有廣泛的適用性.
Ⅲ.類比猜想 探究性質(zhì)
問題8:加法其實(shí)我們并不陌
6、生����,從小就開始學(xué)習(xí)數(shù)��、字母�����、式的加法�����,實(shí)數(shù)的加法有哪些運(yùn)算性質(zhì)���?向量的加法是否也滿足類似的性質(zhì)�����?如果滿足���,具體形式是什么�?
實(shí)數(shù)的加法
向量的加法
性
質(zhì)
交換律的驗(yàn)證讓學(xué)生通過畫圖自己驗(yàn)證����,結(jié)合律的驗(yàn)證師生借助于多媒體共同完成.
研究結(jié)果表明:向量的加法也滿足交換律和結(jié)合律,這與數(shù)的加法是一致的.有了交換律與結(jié)合律�����,向量的加法就可以按任意的組合與任意的次序進(jìn)行�����,從而豐富了向量加法的內(nèi)涵.
Ⅳ.?dāng)?shù)學(xué)運(yùn)用 深化認(rèn)識(shí)
例1.如圖�����,O為正六邊形A1A2A3A4A5A6的中心����,作出下列向量:
(1) (2) (3)
(4)
7���、(5)
推廣1:
推廣2:
并以北京08奧運(yùn)圣火的傳遞提供了現(xiàn)實(shí)原型.
最后我們?cè)倩氐竭@座宏偉壯觀的大橋來解決這樣一個(gè)實(shí)際問題:
例2.已知橋是南北方向,受落潮影響����,海水以12.5km/h的速度向東流,現(xiàn)有一艘工作艇�,在海面上航行檢查橋墩的狀況,已知艇的速度是25km/h��,若艇要沿著與橋平行的方向由南向北航行���,則艇的航向如何確定?
分析:首先將實(shí)際問題數(shù)學(xué)化�����,把三個(gè)速度分別用向量來表示:如圖�����,設(shè)表示水流速度��,表示游艇的速度,那誰是游艇的實(shí)際速度���?�����,三個(gè)向量應(yīng)滿足什么關(guān)系����?.
解:如圖����,設(shè)表示水流速度,表示游艇的速度���,表示游艇的實(shí)際速度�����,因?yàn)?��,所以四邊形為平行四邊形?
在中,
8����、
����, �,
所以
答 若艇要沿著與橋平行的方向由南向北航行,其航向應(yīng)為北偏西.
Ⅴ.回顧反思 拓展延伸
一����、課時(shí)小結(jié):
1、同學(xué)們想一想:本節(jié)課你有些什么收獲呢����?
知識(shí)內(nèi)容:向量加法的定義、二個(gè)運(yùn)算法則以及二個(gè)運(yùn)算律.
留給你印象最深的是什么����?作為課堂的延伸,你課后還想作些什么探究����?
本節(jié)課我們從物理原型抽象出數(shù)學(xué)模型�����,在此基礎(chǔ)上去研究數(shù)學(xué)模型,最后應(yīng)用到生活實(shí)踐中去.再一次告訴我們�����,數(shù)學(xué)源于生活�,又服務(wù)于生活.
2、馬克思說過:一種科學(xué)只有在成功地運(yùn)用數(shù)學(xué)時(shí)����,才算達(dá)到完善的地步. 我們今天所學(xué)習(xí)的向量的加法為研究物理的相關(guān)問題提供了一種數(shù)學(xué)工具,隨著對(duì)向量研究的逐步深入���,向量作為一種新的數(shù)學(xué)工具被越來越廣泛的應(yīng)用.
二�����、拓展延伸:
(1)作業(yè):P79 習(xí)題2.2的1����,2����,3
(2)拓展探究:請(qǐng)同學(xué)們課后完成下面的拓展探究題:向量和的模與模的和之間有什么關(guān)系?(是任意兩個(gè)向量��,則與之間有什么關(guān)系? 并根據(jù)自己感興趣的話題進(jìn)行拓展探究.
 陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 向量的加法教案 北師大版必修4(通用)
陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 向量的加法教案 北師大版必修4(通用)