《2020高考數(shù)學(xué) 核心考點(diǎn) 第3課時(shí) 函數(shù)與方程復(fù)習(xí)（無答案）》由會(huì)員分享，可在線閱讀，更多相關(guān)《2020高考數(shù)學(xué) 核心考點(diǎn) 第3課時(shí) 函數(shù)與方程復(fù)習(xí)（無答案）（2頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、第3課時(shí) 函數(shù)與方程
1．若x0是方程式lgx＋x＝2的解，則x0屬于區(qū)間( )
A．(0,1) B．(1,1.25)
C．(1.25,1.75) D．(1.75,2)
2．(2020年陜西)方程|x|＝cosx在(－∞，＋∞)內(nèi)( )
A．沒有根 B．有且僅有一個(gè)根
C．有且僅有兩個(gè)根 D．有無窮多個(gè)根
3．(2020年湖北)若定義在R上的偶函數(shù)f(x)和奇函數(shù)g(x)滿足f(x)＋g(x)＝ex，則g(x)＝( )
A．ex－e－x B. C. D.
4．(2020年福建)已知函數(shù)f(x)＝，若f(a)＋f(1)＝0，則實(shí)數(shù)a的值等于(
2、 )
A．－3 B．－1 C．1 D．3
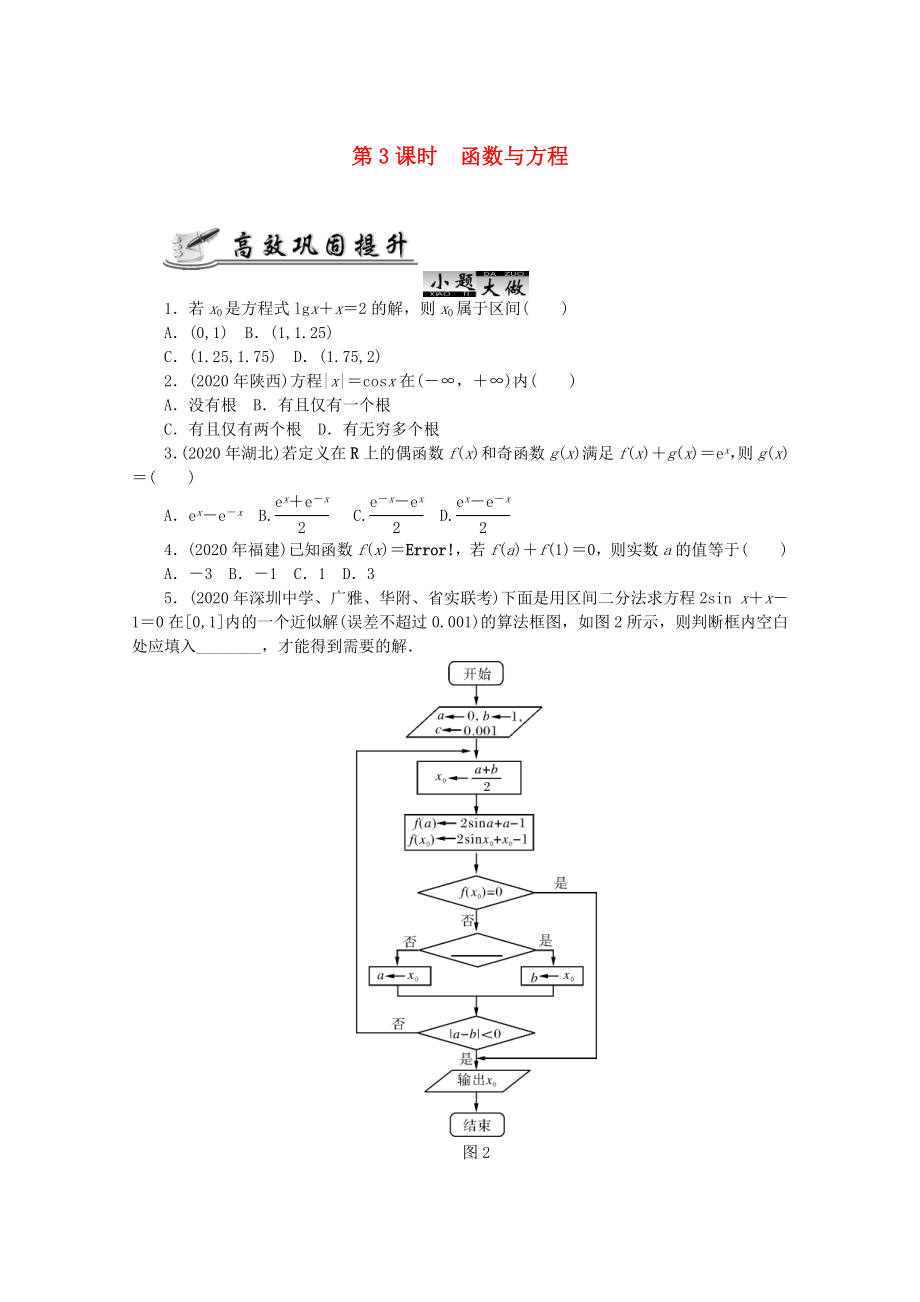
5．(2020年深圳中學(xué)、廣雅、華附、省實(shí)聯(lián)考)下面是用區(qū)間二分法求方程2sin x＋x－1＝0在[0,1]內(nèi)的一個(gè)近似解(誤差不超過0.001)的算法框圖，如圖2所示，則判斷框內(nèi)空白處應(yīng)填入________，才能得到需要的解．
圖2
6．(2020年湖南)已知函數(shù)f(x)＝ex－1，g(x)＝－x2＋4x－3，若有f(a)＝g(b)，則b的取值范圍為( )
A．[2－，2＋] B．(2－，2＋)
C．[1,3] D．(1,3)
7．(2020年山東)已知函數(shù)f(x)＝logax＋x－b(a>0，且a≠1)．當(dāng)2＜
3、a＜3＜b＜4時(shí)，函數(shù)f(x)的零點(diǎn)x0∈(n，n＋1)，n∈N*，則n＝________.
8．(2020年陜西)設(shè)n∈N＋，一元二次方程x2－4x＋n＝0有整數(shù)根的充要條件是n＝________.
9．設(shè)函數(shù)f(x)＝x|x－1|＋m，g(x)＝lnx.
(1)當(dāng)m>1時(shí)，求函數(shù)y＝f(x)在[0，m]上的最大值；
(2)記函數(shù)p(x)＝f(x)－g(x)，若函數(shù)p(x)有零點(diǎn)，求m的取值范圍．
10．(2020年湖北)提高過江大橋的車輛通行能力可改善整個(gè)城市的交通狀況．在一般情況下，大橋上的車流速度v(單位：千米/小時(shí))是車流密度x(單位：輛/千米)的函數(shù)．當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí)，造成堵塞，此時(shí)車流速度為0；當(dāng)車流密度不超過20輛/千米時(shí)，車流速度為60千米/小時(shí)．研究表明：當(dāng)20≤x≤200時(shí)，車流速度v是車流密度x的一次函數(shù)．
(1)當(dāng)0≤x≤200時(shí)，求函數(shù)v(x)的表達(dá)式；
(2)當(dāng)車流密度x為多大時(shí)，車流量(單位時(shí)間內(nèi)通過橋上某觀測(cè)點(diǎn)的車輛數(shù)，單位：輛/小時(shí))f(x)＝x·v(x)可以達(dá)到最大，并求出最大值(精確到1輛/小時(shí))．
2020高考數(shù)學(xué) 核心考點(diǎn) 第3課時(shí) 函數(shù)與方程復(fù)習(xí)（無答案）
