《河北省正定中學(xué)2020屆高考數(shù)學(xué)一輪復(fù)習(xí) 函數(shù)的奇偶性與周期性學(xué)案 理(無答案)》由會員分享��,可在線閱讀�,更多相關(guān)《河北省正定中學(xué)2020屆高考數(shù)學(xué)一輪復(fù)習(xí) 函數(shù)的奇偶性與周期性學(xué)案 理(無答案)(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
1、2.4函數(shù)的奇偶性與周期性
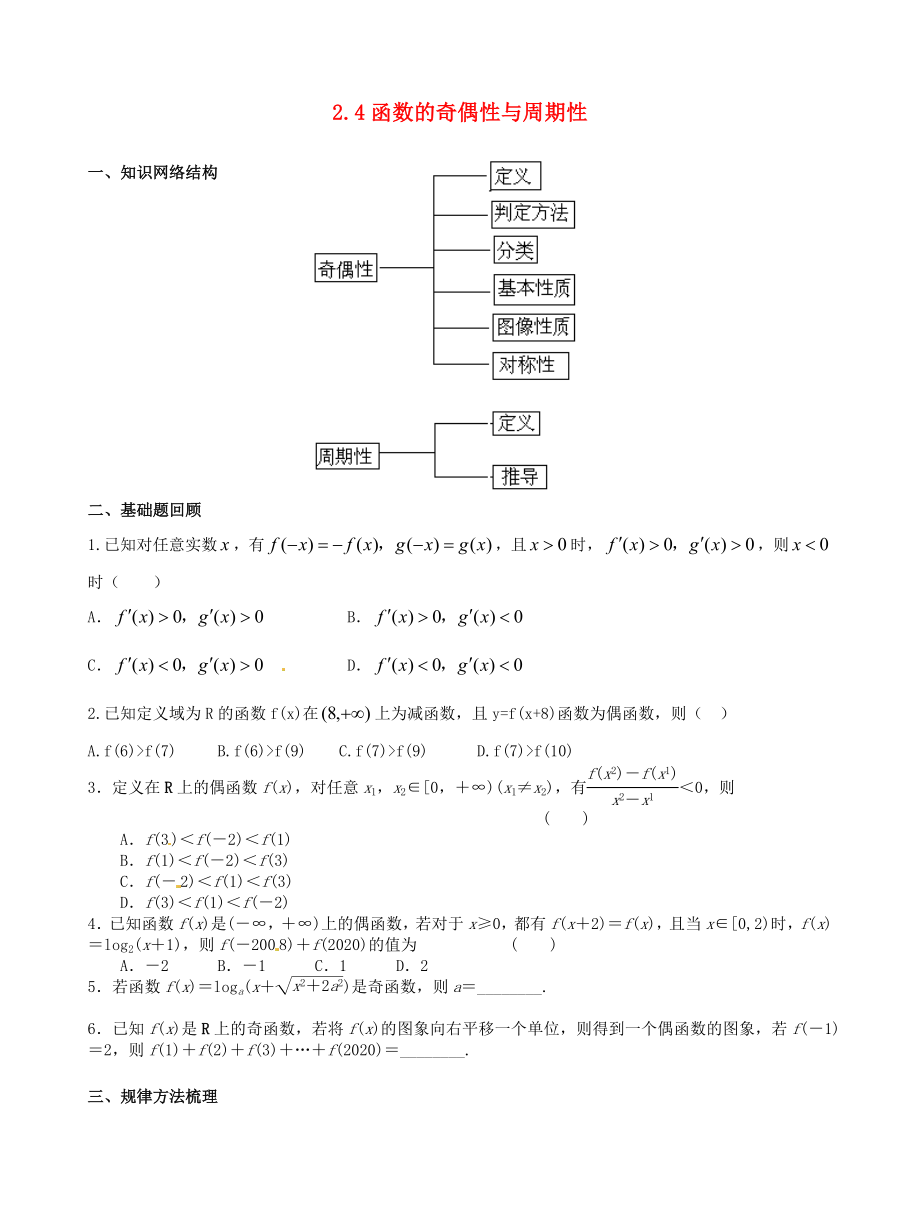
一�、知識網(wǎng)絡(luò)結(jié)構(gòu)
二、基礎(chǔ)題回顧
1.已知對任意實(shí)數(shù)��,有��,且時����,,則時( )
A. B.
C. D.
2.已知定義域?yàn)镽的函數(shù)f(x)在上為減函數(shù)�����,且y=f(x+8)函數(shù)為偶函數(shù)�����,則( )
A.f(6)>f(7) B.f(6)>f(9) C.f(7)>f(9) D.f(7)>f(10)
3.定義在R上的偶函數(shù)f(x)�����,對任意x1�����,x2∈[0����,+∞)(x1≠x2),有<0���,則 ( )
A.f(3)<f(-2)<f(1)
2�����、B.f(1)<f(-2)<f(3)
C.f(-2)<f(1)<f(3)
D.f(3)<f(1)<f(-2)
4.已知函數(shù)f(x)是(-∞���,+∞)上的偶函數(shù)����,若對于x≥0�����,都有f(x+2)=f(x)��,且當(dāng)x∈[0,2)時���,f(x)=log2(x+1)���,則f(-2008)+f(2020)的值為 ( )
A.-2 B.-1 C.1 D.2
5.若函數(shù)f(x)=loga(x+)是奇函數(shù),則a=________.
6.已知f(x)是R上的奇函數(shù)���,若將f(x)的圖象向右平移一個單位��,則得到一個偶函數(shù)的圖象���,若f(-1)=2,則f(1)+f(2)+f(3)+…+f(2
3���、020)=________.
三����、規(guī)律方法梳理
1.奇偶性是函數(shù)在定義域上的整體性質(zhì)����,因此討論函數(shù)奇偶性首先要看其定義域.函數(shù)具有奇偶性的必要條件是其定義域關(guān)于原點(diǎn)對稱,一個函數(shù)是奇(偶)函數(shù)的充要條件是其函數(shù)圖象關(guān)于原點(diǎn)(軸)對稱.
2.奇偶性定義是判斷函數(shù)奇偶性的主要方法之一�����,為了便于判斷�����,有時需要將函數(shù)進(jìn)行化簡���,或應(yīng)用定義的變形式:
?
3.解題中要注意以下性質(zhì)的靈活運(yùn)用:
(1)為偶函數(shù)?���;
(2)若奇函數(shù)在處有定義��,則.
4.函數(shù)周期性問題應(yīng)牢牢把握周期函數(shù)的定義�,并掌握一些常見的確定函數(shù)周期的條件.
5.周期函數(shù)不一定有最小正周期�, 例
6. 設(shè)為非零常數(shù)
4、����,若對定義域內(nèi)的任意,恒有下列條件之一成立:
①����;②;③����;④;⑤��;⑥���,則是周期函數(shù)���,是它的一個周期.
(上述式子分母不為零)
四、典型例題
例1.設(shè)是奇函數(shù),()且f(1)=2��,f(2)<3���,則a=________,b=________��,c=________.
例2.已知函數(shù)y=f(x)是定義在R上的奇函數(shù)�����,則下列函數(shù)中是偶函數(shù)的是 ( )
①y=f(|x|)����;②y=f(-x);③y=x·f(x)��;④y=f(x)+x.
A.①③ B.②③ C.①④ D.②④
例3.已知偶函數(shù)y=f(x)滿足條件��,且當(dāng)x∈[-1,0]時�,,則的值等于________.
5�����、例4.已知函數(shù)f(x)=1-(a>0且a≠1)是定義在(-∞,+∞)上的奇函數(shù).
(1)求a的值�����;
(2)求函數(shù)f(x)的值域��;
(3)當(dāng)x∈(0,1]時���,tf(x)≥2x-2恒成立��,求實(shí)數(shù)t的取值范圍.
五����、反饋練習(xí)
1.命題甲:已知函數(shù)f(x)滿足f(1+x)=f(1-x)�����,則f(x)的圖象關(guān)于直線x=1對稱�;命題乙:函數(shù)f(1+x)與函數(shù)f(1-x)的圖象關(guān)于直線x=1對稱,則 ( )
A.甲真乙假 B.甲假乙真
C.甲����、乙均真 D.甲、乙均假
2.函數(shù)的圖象大致為( )
3.設(shè)是連續(xù)的偶函數(shù),且當(dāng)時是單調(diào)函數(shù),則滿足的所有之和為( )
A. B. C. D.
4.定義在R上的奇函數(shù)y=f(x)����,它的周期為T(T>0)�,則=________.
5.已知函數(shù)
(1)判斷的奇偶性���,并說明理由
(2)當(dāng)時�����,討論函數(shù)在區(qū)間上的單調(diào)性.
 河北省正定中學(xué)2020屆高考數(shù)學(xué)一輪復(fù)習(xí) 函數(shù)的奇偶性與周期性學(xué)案 理(無答案)
河北省正定中學(xué)2020屆高考數(shù)學(xué)一輪復(fù)習(xí) 函數(shù)的奇偶性與周期性學(xué)案 理(無答案)