高中數(shù)學(xué) 第五章 第3課時(shí)《選擇結(jié)構(gòu)》教案（學(xué)生版） 蘇教版必修3

《高中數(shù)學(xué) 第五章 第3課時(shí)《選擇結(jié)構(gòu)》教案（學(xué)生版） 蘇教版必修3》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué) 第五章 第3課時(shí)《選擇結(jié)構(gòu)》教案（學(xué)生版） 蘇教版必修3（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

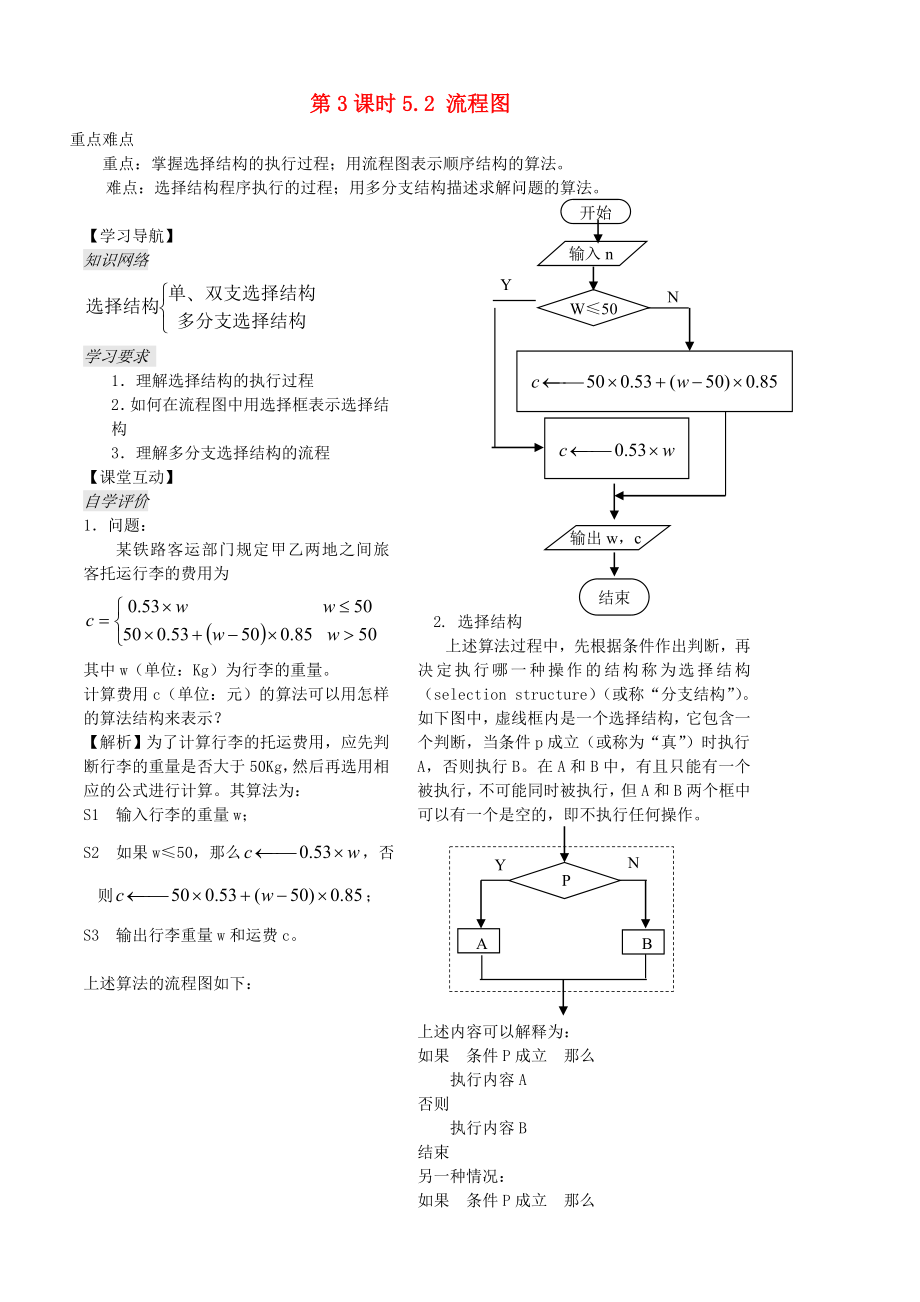
1、第3課時(shí)5.2 流程圖 重點(diǎn)難點(diǎn) 重點(diǎn)：掌握選擇結(jié)構(gòu)的執(zhí)行過(guò)程；用流程圖表示順序結(jié)構(gòu)的算法。 難點(diǎn)：選擇結(jié)構(gòu)程序執(zhí)行的過(guò)程；用多分支結(jié)構(gòu)描述求解問(wèn)題的算法。 【學(xué)習(xí)導(dǎo)航】 知識(shí)網(wǎng)絡(luò) 學(xué)習(xí)要求 1．理解選擇結(jié)構(gòu)的執(zhí)行過(guò)程 2．如何在流程圖中用選擇框表示選擇結(jié)構(gòu) 3．理解多分支選擇結(jié)構(gòu)的流程 【課堂互動(dòng)】 自學(xué)評(píng)價(jià) 1．問(wèn)題： 某鐵路客運(yùn)部門規(guī)定甲乙兩地之間旅客托運(yùn)行李的費(fèi)用為 其中w（單位：Kg）為行李的重量。 計(jì)算費(fèi)用c（單位：元）的算法可以用怎樣的算法結(jié)構(gòu)來(lái)表示？ 【解析】為了計(jì)算行李的托運(yùn)費(fèi)用，應(yīng)先判斷行李的重量是否大于50Kg，然后再選用

2、相應(yīng)的公式進(jìn)行計(jì)算。其算法為： S1 輸入行李的重量w； S2 如果w≤50，那么，否則； S3 輸出行李重量w和運(yùn)費(fèi)c。 上述算法的流程圖如下： 開始 輸入n W≤50 Y 結(jié)束 N 輸出w，c 2. 選擇結(jié)構(gòu) 上述算法過(guò)程中，先根據(jù)條件作出判斷，再?zèng)Q定執(zhí)行哪一種操作的結(jié)構(gòu)稱為選擇結(jié)構(gòu)（selection structure）（或稱“分支結(jié)構(gòu)”）。如下圖中，虛線框內(nèi)是一個(gè)選擇結(jié)構(gòu)，它包含一個(gè)判斷，當(dāng)條件p成立（或稱為“真”）時(shí)執(zhí)行A，否則執(zhí)行B。

3、在A和B中，有且只能有一個(gè)被執(zhí)行，不可能同時(shí)被執(zhí)行，但A和B兩個(gè)框中可以有一個(gè)是空的，即不執(zhí)行任何操作。 N Y P A B 上述內(nèi)容可以解釋為： 如果 條件P成立 那么 執(zhí)行內(nèi)容A 否則 執(zhí)行內(nèi)容B 結(jié)束 另一種情況： 如果 條件P成立 那么 執(zhí)行內(nèi)容A 結(jié)束 Y P 用框圖可表示為： N A 【經(jīng)典范例】 例1 任意給定三個(gè)正實(shí)數(shù)，設(shè)計(jì)一個(gè)算法，判斷：以這樣三個(gè)數(shù)為邊長(zhǎng)的三角形是否存在？畫出它的流程圖。 分析 要判定三個(gè)實(shí)數(shù)能否構(gòu)成三角形的三條邊，主要是根據(jù)三角形的邊角關(guān)系定理：任意兩邊之和大于第三邊。即如果

4、三個(gè)數(shù)中的任意兩個(gè)之和大于第三個(gè)數(shù)，那么它們就可以作為三角形的三條邊長(zhǎng)。 【解】流程圖： 例2 設(shè)計(jì)求解一元二次方程 的一個(gè)算法，并用流程圖表示。 【解】算法如下 S1 輸入a，b，c S2 △ S3 如果△＜0，那么輸出“由于方程無(wú)實(shí)數(shù)根”，否則，，輸出這兩個(gè)根。 流程圖： 例3 如果考生的成績(jī)大于或等于60分，則輸出“及格”，否則輸出“不及格”，用流程圖表示這一算法過(guò)程。 【解】

5、 追蹤訓(xùn)練一 1、如果考生的成績(jī) (以滿分100分計(jì)) ,則輸出“優(yōu)秀”；若成績(jī)，則輸出“中等”；若，則輸出“及格”；若，則輸出“不及格”。若輸入的成績(jī)?yōu)?5,則輸出結(jié)果為______________。 2、下邊的流程圖（如圖所示），能判斷任意輸入的數(shù)x的奇偶性，其中判斷框內(nèi)的條件是 . 開始 輸入a，b，c a>b且a>c b>c Y N Y N 輸出a 輸出c 輸出b 結(jié)束 3、下面的流程圖表示了一個(gè)什么樣的算法？ 【解】 思考：如果要實(shí)現(xiàn)上述流程圖所表示的目的，是否還有其它的算法？ 算法：將a與b進(jìn)行比較，將大的數(shù)放入一個(gè)臨時(shí)變量Max中，再將Max與c比較，輸出大的數(shù)。 4、寫出解方程（a，b為常數(shù)）的算法，并畫出流程圖。 【解】算法如下： 流程圖開始 輸入a，b a=0 N 結(jié)束 Y 方程無(wú)解 : 5、設(shè)計(jì)一個(gè)求任意實(shí)數(shù)的絕對(duì)值的算法，并畫出流程圖． 【解】算法如下： S1 輸入任意實(shí)數(shù)； S2 若，則；否則； S3 輸出． 流程圖如下：