2020屆高考數(shù)學(xué)二輪復(fù)習(xí) 專題3 立體幾何 第1講 空間幾何體的表面積與體積練習(xí) 理

《2020屆高考數(shù)學(xué)二輪復(fù)習(xí) 專題3 立體幾何 第1講 空間幾何體的表面積與體積練習(xí) 理》由會員分享，可在線閱讀，更多相關(guān)《2020屆高考數(shù)學(xué)二輪復(fù)習(xí) 專題3 立體幾何 第1講 空間幾何體的表面積與體積練習(xí) 理（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

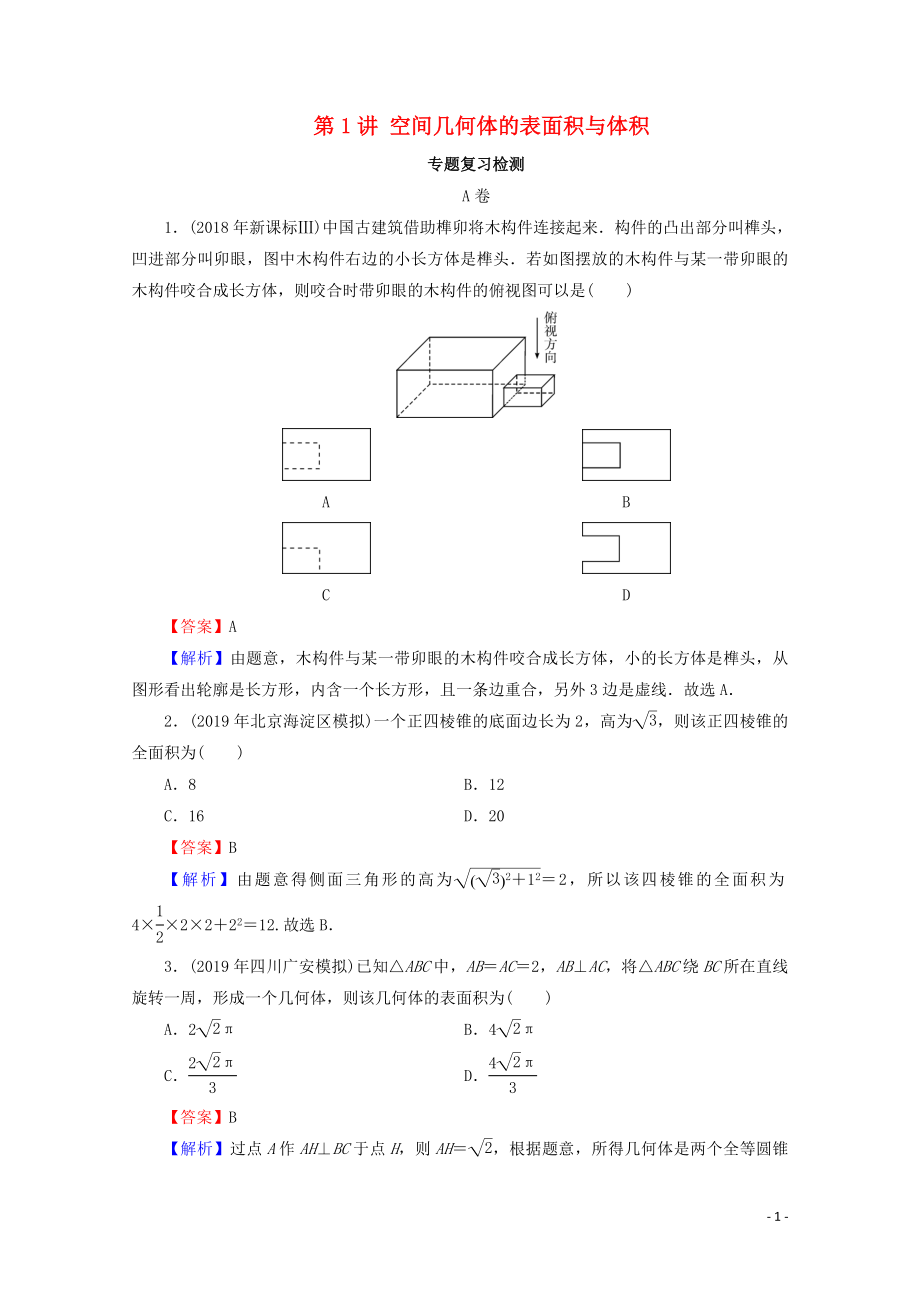
1、第1講 空間幾何體的表面積與體積 專題復(fù)習(xí)檢測 A卷 1．(2018年新課標(biāo)Ⅲ)中國古建筑借助榫卯將木構(gòu)件連接起來．構(gòu)件的凸出部分叫榫頭，凹進(jìn)部分叫卯眼，圖中木構(gòu)件右邊的小長方體是榫頭．若如圖擺放的木構(gòu)件與某一帶卯眼的木構(gòu)件咬合成長方體，則咬合時帶卯眼的木構(gòu)件的俯視圖可以是(　　) A B C D 【答案】A 【解析】由題意，木構(gòu)件與某一帶卯眼的木構(gòu)件咬合成長方體，小的長方體是榫頭，從圖形看出輪廓是長方形，內(nèi)含一個長方形，且一條邊重合，另外3邊是虛線．故選A． 2．(2019年北京海淀區(qū)模擬)一個正四棱錐的底面邊長為2，高為，則該正四棱錐的全面積為(　　) A

2、．8　 B．12　　 C．16　 D．20 【答案】B 【解析】由題意得側(cè)面三角形的高為＝2，所以該四棱錐的全面積為4××2×2＋22＝12.故選B． 3．(2019年四川廣安模擬)已知△ABC中，AB＝AC＝2，AB⊥AC，將△ABC繞BC所在直線旋轉(zhuǎn)一周，形成一個幾何體，則該幾何體的表面積為(　　) A．2π　 B．4π　　　　 C．　 D． 【答案】B 【解析】過點(diǎn)A作AH⊥BC于點(diǎn)H，則AH＝，根據(jù)題意，所得幾何體是兩個全等圓錐底面相接而成的組合體，圓錐底面半徑為r＝，母線長為l＝2，所以表面積為S＝2πrl＝4π.故選B． 4．如圖，直三棱柱ABC－A1B1C1的六

3、個頂點(diǎn)都在半徑為1的半球面上，AB＝AC，側(cè)面BCC1B1是半球底面圓的內(nèi)接正方形，則側(cè)面ABB1A1的面積為(　　) A．2　 B．1　　 C．　 D． 【答案】C 【解析】連接BC1，B1C交于點(diǎn)O，則O為平面BCC1B1的中心且BC1⊥B1C.由題意知，球心為O，BC為截面圓的直徑，所以∠BAC＝90°.設(shè)正方形BCC1B1的邊長為x，在Rt△OB1C1中，OC1＝OB1＝R＝1(R為球的半徑)，所以x＝＝，則AB＝AC＝1.所以側(cè)面ABB1A1的面積為×1＝.故選C． 5．(2019年江蘇)如圖，長方體ABCD－A1B1C1D1的體積是120，E為CC1的中點(diǎn)，則三棱

4、錐E－BCD的體積是________． 【答案】10 【解析】由題意，VABCD－A1B1C1D1＝AB·BC·DD1＝120，VE－BCD＝S△BCD·CE＝×·BC·DC·CE＝AB·BC·DD1＝10. 6．(2019年北京)某幾何體是由一個正方體去掉一個四棱柱所得，其三視圖如圖所示．如果網(wǎng)格紙上小正方形的邊長為1，那么該幾何體的體積為________． 【答案】40 【解析】由三視圖還原原幾何體如圖，該幾何體可看作是兩個四棱柱的組合體，則該幾何體的體積V＝×4＝40. B卷 7．某幾何體的三視圖如圖所示，則該幾何體的表面積為(　　) A．18＋2π　　

5、B．20＋π C．20＋　　　　 D．16＋π 【答案】B 【解析】由三視圖知該幾何體是一個邊長為2的正方體割去了相對邊對應(yīng)的兩個半徑為1、高為1的圓柱體，其表面積相當(dāng)于正方體五個面的面積與兩個圓柱的側(cè)面積的和，即該幾何體的表面積S＝4×5＋2×2π×1×1×＝20＋π. 8．(2019年新課標(biāo)Ⅱ)中國有悠久的金石文化，印信是金石文化的代表之一．印信的形狀多為長方體、正方體或圓柱體，但南北朝時期的官員獨(dú)孤信的印信形狀是“半正多面體”(圖1)．半正多面體是由兩種或兩種以上的正多邊形圍成的多面體．半正多面體體現(xiàn)了數(shù)學(xué)的對稱美．圖2是一個棱數(shù)為48的半正多面體，它的所有頂點(diǎn)都在同一個正方體

6、的表面上，且此正方體的棱長為1.則該半正多面體共有________個面，其棱長為________． 　　 【答案】26　－1 【解析】該半正多面體共有8＋8＋8＋2＝26個面，設(shè)其棱長為x，則x＋x＋x＝1，解得x＝－1. 9．(2018年江蘇南通三模)在菱形ABCD中，A＝，AB＝4，將△ABD沿BD折起到△PBD的位置，若取BD中點(diǎn)為E，此時∠PEC＝，三棱錐P－BCD的外接球心為O，則三棱錐P－BCD的外接球的表面積為________． 【答案】112π 【解析】∵四邊形ABCD是菱形，A＝，∴△BCD是等邊三角形．如圖，過球心O作OO′⊥平面BCD，則O′為等邊△BCD的中心，BD的中點(diǎn)為E，連接PO.易證△POE≌△COE，由∠PEC＝，得∠OEC＝.∵AB＝4，∴AE＝EC＝6，EO′＝EC＝2.在Rt△OEO′中，由∠OEO′＝，得OE＝4.在△OEC中，OC2＝OE2＋EC2－2OE·EC·cos∠OEC＝28，即OC＝2.∴三棱錐P－BCD的外接球的半徑為R＝2，表面積S＝4πR2＝112π. - 5 -