【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第14課時 三角形與全等三角形模擬預測

《【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第14課時 三角形與全等三角形模擬預測》由會員分享，可在線閱讀，更多相關《【優(yōu)化設計】（福建專版）2015中考數(shù)學總復習 第14課時 三角形與全等三角形模擬預測（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

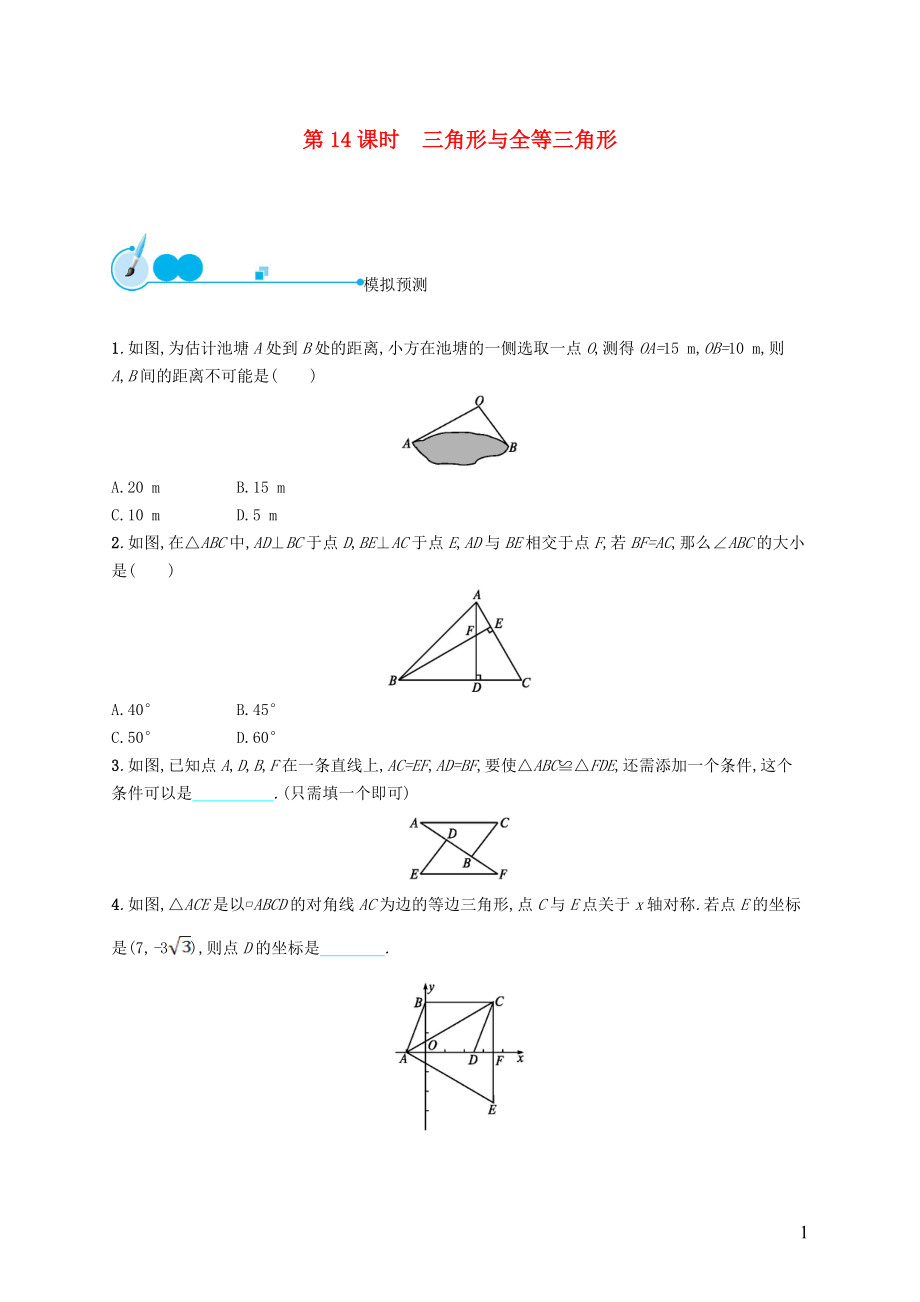
1、 第14課時　三角形與全等三角形 模擬預測 1.如圖,為估計池塘A處到B處的距離,小方在池塘的一側(cè)選取一點O,測得OA=15 m,OB=10 m,則A,B間的距離不可能是(　　) A.20 m B.15 m C.10 m D.5 m 2.如圖,在△ABC中,AD⊥BC于點D,BE⊥AC于點E,AD與BE相交于點F,若BF=AC,那么∠ABC的大小是(　　) A.40° B.45° C.50° D.60° 3.如圖,已知點A,D,B,F在一條直線上,AC=EF,AD=BF,要使△ABC≌△FDE,還需添加一個條件,這個條件可以是　　　　　.(只需填一個即可)

2、? 4.如圖,△ACE是以?ABCD的對角線AC為邊的等邊三角形,點C與E點關于x軸對稱.若點E的坐標是(7,-3),則點D的坐標是　　　　.? 5.如圖,在△ABC中,CD是∠ACB的平分線,∠A=80°,∠ACB=60°,那么∠BDC=　　　　　.? 6.在邊長為1的等邊△ABC中,中線AD與中線BE相交于點O,則OA長度為　　　　.? 7.若P為△ABC所在平面上一點,且∠APB=∠BPC=∠CPA=120°,則點P叫做△ABC的費馬點. (1)若點P為銳角△ABC的費馬點,且∠ABC=60°,PA=3,PC=4,則PB的值為　　　　　;? (2)如圖,在

3、銳角△ABC外側(cè)作等邊△ACB',連接BB'.求證:BB'過△ABC的費馬點P,且BB'=PA+PB+PC. 答案 1.D 2.B　因為AD⊥BC于點D,BE⊥AC于點E, 所以∠EBC+∠C=∠FBD+∠BFD=90°. 所以∠C=∠BFD. 從而得△BFD≌△ACD,則AD=BD, 所以∠ABD=∠BAD=45°,故選B. 3.∠A=∠F(答案不唯一) 4.(5,0) 5.110° 6.　連接DE,∵點D,點E分別為邊BC,AC的中點, ∴DE􀰿AB.∴△DOE∽△AOB. ∴.∴. 在等邊△ABC中,AD

4、為中線, ∴AD⊥BC.∴AD=AC·sin 60°=. ∴OA=AD=. 7.解:(1)2 (2)證明在BB'上取點P,使∠BPC=120°,連接AP,再在PB'上截取PE=PC,連接CE. ∵∠BPC=120°, ∴∠EPC=60°. ∴△PCE為正三角形. ∴PC=CE,∠PCE=60°,∠CEB'=120°. ∵△ACB'為正三角形, ∴AC=B'C,∠ACB'=60°. ∴∠PCA+∠ACE=∠ACE+∠ECB'=60°. ∴∠PCA=∠ECB'. ∴△ACP≌△B'CE. ∴∠APC=∠B'EC=120°,PA=EB'. ∴∠APB=∠APC=∠BPC=120°. ∴P為△ABC的費馬點, ∴BB'過△ABC的費馬點P, 且BB'=EB'+PB+PE=PA+PB+PC. 3