2019版中考數(shù)學(xué)專題復(fù)習(xí) 專題六 圓（23）第1課時(shí) 圓的有關(guān)性質(zhì)當(dāng)堂達(dá)標(biāo)題

《2019版中考數(shù)學(xué)專題復(fù)習(xí) 專題六 圓（23）第1課時(shí) 圓的有關(guān)性質(zhì)當(dāng)堂達(dá)標(biāo)題》由會(huì)員分享，可在線閱讀，更多相關(guān)《2019版中考數(shù)學(xué)專題復(fù)習(xí) 專題六 圓（23）第1課時(shí) 圓的有關(guān)性質(zhì)當(dāng)堂達(dá)標(biāo)題（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

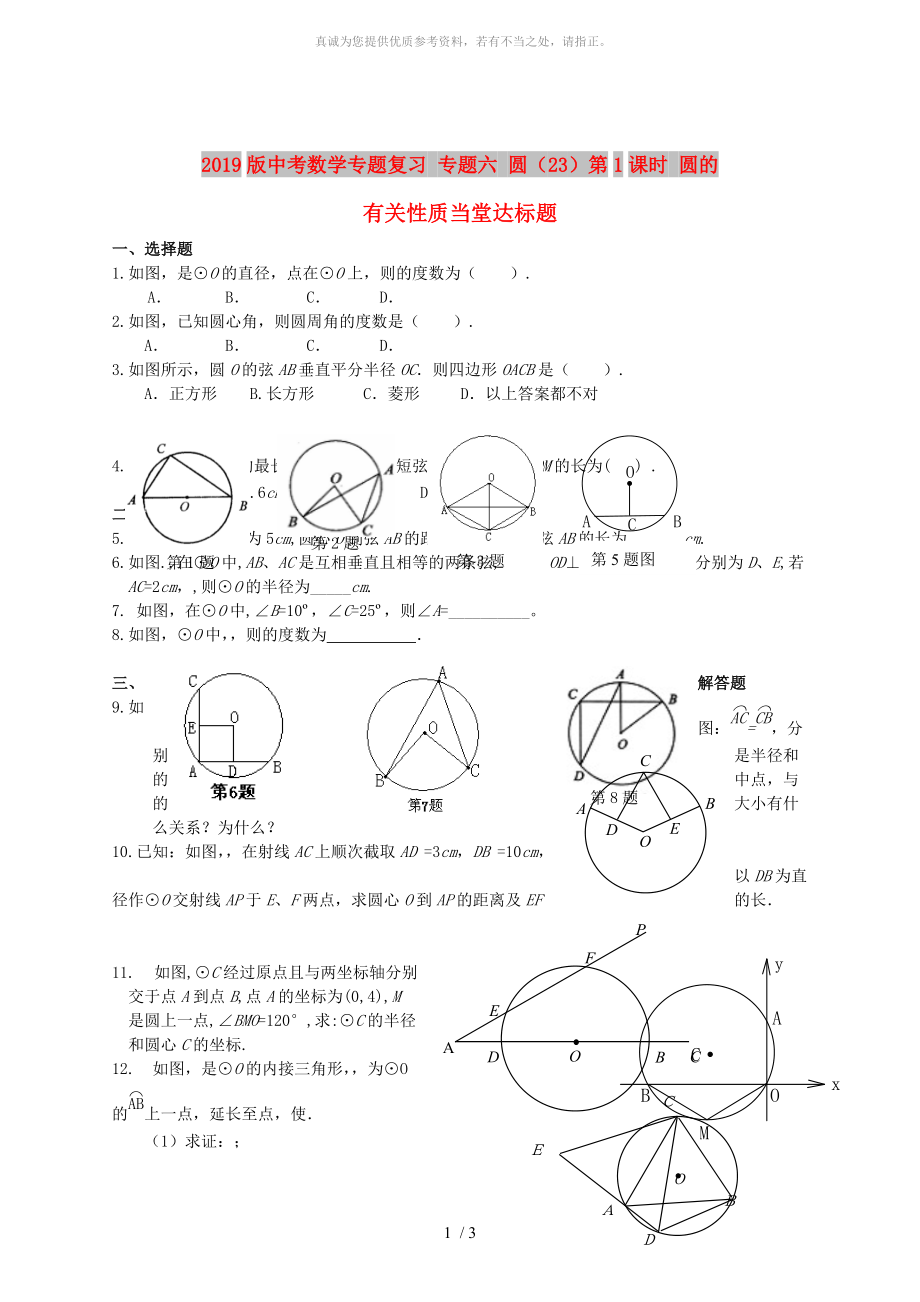
1、 真誠(chéng)為您提供優(yōu)質(zhì)參考資料，若有不當(dāng)之處，請(qǐng)指正。 2019版中考數(shù)學(xué)專題復(fù)習(xí) 專題六 圓（23）第1課時(shí) 圓的 有關(guān)性質(zhì)當(dāng)堂達(dá)標(biāo)題 一、選擇題 1.如圖，是⊙O的直徑，點(diǎn)在⊙O上，則的度數(shù)為（ ）. A． B． C． D． 2.如圖，已知圓心角，則圓周角的度數(shù)是（ ）. A． B． C． D． 3.如圖所示，圓O的弦AB垂直平分半徑OC．則四邊形OACB是（　?。? A．正方形 B.長(zhǎng)方形 C．菱形 D．以上答案都不對(duì) 第2題 第3題 第1題 第5題圖 第1題 4.過⊙O內(nèi)一點(diǎn)M

2、的最長(zhǎng)弦長(zhǎng)為10cm,最短弦長(zhǎng)為8cm,那么OM的長(zhǎng)為( ) . A.3cm B.6cm C. cm D.9cm 二、填空題 5.如圖,⊙O的半徑為5cm,圓心O到弦AB的距離為3cm, 則弦AB的長(zhǎng)為_______cm. 6.如圖.,在⊙O中,AB、AC是互相垂直且相等的兩條弦, OD⊥AB,OE⊥AC,垂足分別為D、E,若AC=2cm，,則⊙O的半徑為_____cm. 7. 如圖，在⊙O中,∠B=10，∠C=25，則∠A=__________。 8.如圖，⊙O中，，則的度數(shù)為 ． 第8題 三、解答題

3、 C B O E D A 9.如圖：=，分別是半徑和的中點(diǎn)，與 的大小有什么關(guān)系？為什么？ 10.已知：如圖，，在射線AC上順次截取AD =3cm，DB =10cm， 以DB為直徑作⊙O交射線AP于E、F兩點(diǎn)，求圓心O到AP的距離及EF 的長(zhǎng)． O A D B C E F P 11. 如圖,⊙C經(jīng)過原點(diǎn)且與兩坐標(biāo)軸分別交于點(diǎn)A到點(diǎn)B,點(diǎn)A的坐標(biāo)為(0,4),M是圓上一點(diǎn),∠BMO=120,求:⊙C的半徑和圓心C的坐標(biāo). Ｃ Ｅ Ａ Ｏ Ｄ Ｂ 12.　如圖，是⊙O的內(nèi)接三角形，，為⊙O的上一點(diǎn)，延長(zhǎng)至點(diǎn)，使． （1）求證：；

4、（2）若，求證：． 圓的有關(guān)性質(zhì)復(fù)習(xí)當(dāng)堂達(dá)標(biāo)題答案 1. D 2. C 3. C 4. A 5. 8 6. 錯(cuò)誤！未找到引用源。7.35 8.50 9. 連接OC， ∵D、E分別是OA、OB的中點(diǎn)， ∴OD=OE， 又∵，∴∠DOC=∠EOC， OC=OC，∴△CDO≌△CEO， ∴CD=CE． 10. 過點(diǎn)O作OG⊥AP于點(diǎn)G， 連接OF， ∵DB=10， ∴OD=5， ∴AO=AD+OD=3+5=8， ∵∠PAC=30， ∴OG= AO= 8=4cm ∵OG⊥EF， ∴EG=GF， ∵GF=， ∴EF=6cm.

5、 11. 連接AB，AM，則由∠AOB=90，故AB是直徑. 由∠BAM+∠OAM=∠BOM+∠OBM=180－120=60，得∠BAO=60. 又∵AO=4，∴. ∴⊙C的半徑為4，. 過C作CE⊥OA于E，CF⊥OB于F，則 . ∴C點(diǎn)坐標(biāo)為（－，2）. 12. （1）在△ABC中，CAB=∠CBA． 在△ECD中，∠E=∠CDE． ∵∠CBA=∠CDE，（同弧上的圓周角相等）， ∴∠E=∠CDE=∠CAB=∠CBA， ∵∠E+∠ECD+∠EDC=180，∠CAB+∠ACB+∠ABC=180， ∴∠ACB=∠ECD， ∴∠ACB-∠ACD=∠ECD-∠ACD． ∴∠ACE=∠BCD， 在△ACE和△BCD中，∠ACE=∠BCD；CE=CD；AC=BC， ∴△ACE≌△BCD． ∴AE=BD； （2）若AC⊥BC，∵∠ACB=∠ECD． ∴∠ECD=90， ∴∠CED=∠CDE=45， ∴DE= CD 又∵AD+BD=AD+EA=ED， ∴AD+BD= CD 3 / 3