新編高三數(shù)學(xué)理,山東版一輪備課寶典 【第10章】課時(shí)限時(shí)檢測65

《新編高三數(shù)學(xué)理,山東版一輪備課寶典 【第10章】課時(shí)限時(shí)檢測65》由會(huì)員分享，可在線閱讀，更多相關(guān)《新編高三數(shù)學(xué)理,山東版一輪備課寶典 【第10章】課時(shí)限時(shí)檢測65（7頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

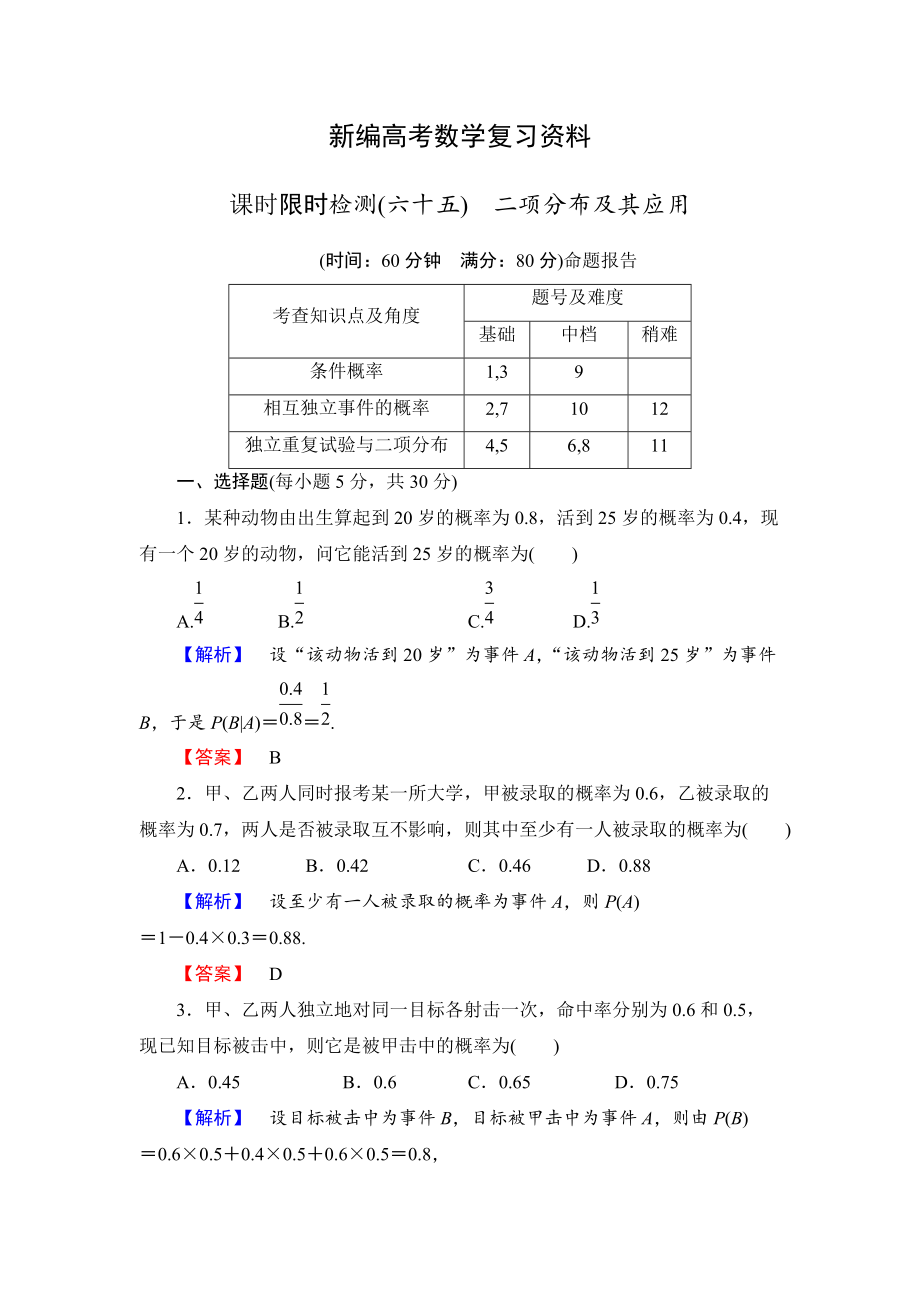
1、新編高考數(shù)學(xué)復(fù)習(xí)資料 課時(shí)限時(shí)檢測(六十五)　二項(xiàng)分布及其應(yīng)用 (時(shí)間：60分鐘　滿分：80分)命題報(bào)告 考查知識(shí)點(diǎn)及角度 題號(hào)及難度 基礎(chǔ) 中檔 稍難 條件概率 1,3 9 相互獨(dú)立事件的概率 2,7 10 12 獨(dú)立重復(fù)試驗(yàn)與二項(xiàng)分布 4,5 6,8 11 一、選擇題(每小題5分，共30分) 1．某種動(dòng)物由出生算起到20歲的概率為0.8，活到25歲的概率為0.4，現(xiàn)有一個(gè)20歲的動(dòng)物，問它能活到25歲的概率為(　　) A.　　　　B.　　　　 C.　 　　　D. 【解析】　設(shè)“該動(dòng)物活到20歲”為事件A，“該動(dòng)物活到25歲”為事件B，于是P(

2、B|A)＝＝. 【答案】　B 2．甲、乙兩人同時(shí)報(bào)考某一所大學(xué)，甲被錄取的概率為0.6，乙被錄取的概率為0.7，兩人是否被錄取互不影響，則其中至少有一人被錄取的概率為(　　) A．0.12 B．0.42 C．0.46 D．0.88 【解析】　設(shè)至少有一人被錄取的概率為事件A，則P(A)＝1－0.4×0.3＝0.88. 【答案】　D 3．甲、乙兩人獨(dú)立地對同一目標(biāo)各射擊一次，命中率分別為0.6和0.5，現(xiàn)已知目標(biāo)被擊中，則它是被甲擊中的概率為(　　) A．0.45 B．0.6 C．0.65 D．0.75 【解析】　

3、設(shè)目標(biāo)被擊中為事件B，目標(biāo)被甲擊中為事件A，則由P(B)＝0.6×0.5＋0.4×0.5＋0.6×0.5＝0.8， 得P(A|B)＝＝＝＝0.75. 【答案】　D 4．位于坐標(biāo)原點(diǎn)的一個(gè)質(zhì)點(diǎn)P按下述規(guī)則移動(dòng)：質(zhì)點(diǎn)每次移動(dòng)一個(gè)單位；移動(dòng)的方向?yàn)橄蛏匣蛳蛴?，并且向上、向右移?dòng)的概率都是.質(zhì)點(diǎn)P移動(dòng)五次后位于點(diǎn)(2,3)的概率是(　　) A.5 B．C5 C．C3 D．CC5 【解析】　由于質(zhì)點(diǎn)每次移動(dòng)一個(gè)單位，移動(dòng)的方向?yàn)橄蛏匣蛳蛴?，移?dòng)五次后位于點(diǎn)(2,3)，所以質(zhì)點(diǎn)P必須向右移動(dòng)兩次，向上移動(dòng)三次，故其概率為C3·2＝C5＝C5，故選B. 【答案】　B 5．如果X～B，

4、則使P(X＝k)取最大值的k值為(　　) A．3 B．4 C．5 D．3或4 【解析】　采取特殊值法． ∵P(X＝3)＝C312，P(X＝4)＝C4·11，P(X＝5)＝C510， 從而易知P(X＝3)＝P(X＝4)＞P(X＝5)． 【答案】　D 6．箱中裝有標(biāo)號(hào)為1,2,3,4,5,6且大小相同的6個(gè)球．從箱中一次摸出兩個(gè)球，記下號(hào)碼并放回，如果兩球號(hào)碼之積是4的倍數(shù)，則獲獎(jiǎng)．現(xiàn)有4人參與摸獎(jiǎng)，恰好有3人獲獎(jiǎng)的概率是(　　) A. B. C. D. 【解析】　若摸出的兩球中含有4，必獲獎(jiǎng)，有5種

5、情形；若摸出的兩球是2,6，也能獲獎(jiǎng)．故獲獎(jiǎng)的情形共6種，獲獎(jiǎng)的概率為＝.現(xiàn)有4人參與摸獎(jiǎng)，恰有3人獲獎(jiǎng)的概率是C3·＝. 【答案】　B 二、填空題(每小題5分，共15分) 7．某籃球隊(duì)員在比賽中每次罰球的命中率相同，且在兩次罰球中至多命中一次的概率為，則該隊(duì)員每次罰球的命中率為________． 【解析】　設(shè)該隊(duì)員每次罰球的命中率為P(0＜P＜1)， 則依題意有1－P2＝，又0＜P＜1，∴P＝. 【答案】　 8．設(shè)隨機(jī)變量X～B(2，p)，隨機(jī)變量Y～B(3，p)，若P(X≥1)＝，則P(Y≥1)＝________. 【解析】　∵X～B(2，p)， ∴P(X≥1)＝1－P(

6、X＝0)＝1－C(1－p)2＝， 解得p＝.又Y～B(3，p)， ∴P(Y≥1)＝1－P(Y＝0)＝1－C(1－p)3＝. 【答案】　 9．(2014·淄博模擬)某學(xué)校一年級(jí)共有學(xué)生100名，其中男生60人，女生40人．來自北京的有20人，其中男生12人，若任選一人是女生，則該女生來自北京的概率是________． 【解析】　設(shè)事件A＝“任選一人是女生”，B＝“任選一人來自北京”，依題意知，來自北京的女生有8人，這是一個(gè)條件概率，問題即計(jì)算P(B|A)． 由于P(A)＝，P(AB)＝， 則P(B|A)＝＝＝. 【答案】　 三、解答題(本大題共3小題，共35分) 10．(10

7、分)(2013·重慶高考)某商場舉行的“三色球”購物摸獎(jiǎng)活動(dòng)規(guī)定：在一次摸獎(jiǎng)中，摸獎(jiǎng)?wù)呦葟难b有3個(gè)紅球與4個(gè)白球的袋中任意摸出3個(gè)球，再從裝有1個(gè)藍(lán)球與2個(gè)白球的袋中任意摸出1個(gè)球．根據(jù)摸出4個(gè)球中紅球與藍(lán)球的個(gè)數(shù)，設(shè)一、二、三等獎(jiǎng)如下： 獎(jiǎng)級(jí) 摸出紅、藍(lán)球個(gè)數(shù) 獲獎(jiǎng)金額 一等獎(jiǎng) 3紅1藍(lán) 200元 二等獎(jiǎng) 3紅0藍(lán) 50元 三等獎(jiǎng) 2紅1藍(lán) 10元 其余情況無獎(jiǎng)且每次摸獎(jiǎng)最多只能獲得一個(gè)獎(jiǎng)級(jí)． (1)求一次摸獎(jiǎng)恰好摸到1個(gè)紅球的概率； (2)求摸獎(jiǎng)?wù)咴谝淮蚊?jiǎng)中獲獎(jiǎng)金額X的分布列與期望E(X)． 【解】　設(shè)Ai(i＝0,1,2,3)表示摸到i個(gè)紅球，Bj(j＝

8、0,1)表示摸到j(luò)個(gè)藍(lán)球，則Ai與Bj獨(dú)立． (1)恰好摸到1個(gè)紅球的概率為 P(A1)＝＝. (2)X的所有可能值為：0,10,50,200，且 P(X＝200)＝P(A3B1)＝P(A3)P(B1)＝·＝， P(X＝50)＝P(A3B0)＝P(A3)P(B0)＝·＝， P(X＝10)＝P(A2B1)＝P(A2)P(B1)＝·＝＝， P(X＝0)＝1－－－＝. 綜上可知，獲獎(jiǎng)金額X的分布列為 X 0 10 50 200 P 從而有E(X)＝0×＋10×＋50×＋200×＝4(元)． 11．(12分)某人拋擲一枚硬幣，出現(xiàn)正、反面的概率都是，構(gòu)

9、造數(shù)列{an}，使an＝Sn＝a1＋a2＋…＋an(n∈N*)． (1)求S8＝2時(shí)的概率； (2)求S2≠0且S8＝2的概率． 【解】　(1)設(shè)出現(xiàn)正面的次數(shù)為ξ，則ξ～B， 由S8＝2知ξ＝5，于是S8＝2的概率為： P(ξ＝5)＝C·53＝C·8＝. (2)S2≠0即前兩次擲硬幣中有2次正面或2次反面， 前2次是正面且S8＝2的概率為： P1＝2·C6＝C8＝， 前2次是反面且S8＝2的概率為： P2＝2C6＝. 故S2≠0且S8＝2的概率為：P＝P1＋P2＝. 12．(13分)(2013·陜西高考)在一場娛樂晚會(huì)上，有5位民間歌手(1至5號(hào))登臺(tái)演唱，由現(xiàn)場數(shù)百

10、名觀眾投票選出最受歡迎歌手．各位觀眾須彼此獨(dú)立地在選票上選3名歌手，其中觀眾甲是1號(hào)歌手的歌迷，他必選1號(hào)，不選2號(hào)，另在3至5號(hào)中隨機(jī)選2名．觀眾乙和丙對5位歌手的演唱沒有偏愛，因此在1至5號(hào)中隨機(jī)選3名歌手． (1)求觀眾甲選中3號(hào)歌手且觀眾乙未選中3號(hào)歌手的概率； (2)X表示3號(hào)歌手得到觀眾甲、乙、丙的票數(shù)之和，求X的分布列及數(shù)學(xué)期望． 【解】　(1)設(shè)A表示事件“觀眾甲選中3號(hào)歌手”，B表示事件“觀眾乙選中3號(hào)歌手”， 則P(A)＝＝，P(B)＝＝. ∵事件A與B相互獨(dú)立， ∴觀眾甲選中3號(hào)歌手且觀眾乙未選中3號(hào)歌手的概率為P(A)＝P(A)·P()＝P(A)·[1－P(B)]＝ ×＝. (2)設(shè)C表示事件“觀眾丙選中3號(hào)歌手”， 則P(C)＝＝， ∵X可能的取值為0,1,2,3，且取這些值的概率分別為 P(X＝0)＝P()＝××＝， P(X＝1)＝P(A)＋P(B)＋P(C)＝××＋××＋××＝＝， P(X＝2)＝P(AB)＋P(AC)＋P(BC)＝××＋××＋××＝＝， P(X＝3)＝P(ABC)＝××＝＝， ∴X的分布列為 X 0 1 2 3 P ∴X的數(shù)學(xué)期望EX＝0×＋1×＋2×＋3×＝＝.