《2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù)能力訓(xùn)練（4）（無(wú)答案）》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù)能力訓(xùn)練（4）（無(wú)答案）（4頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
二次函數(shù)能力訓(xùn)練（4）
姓名：
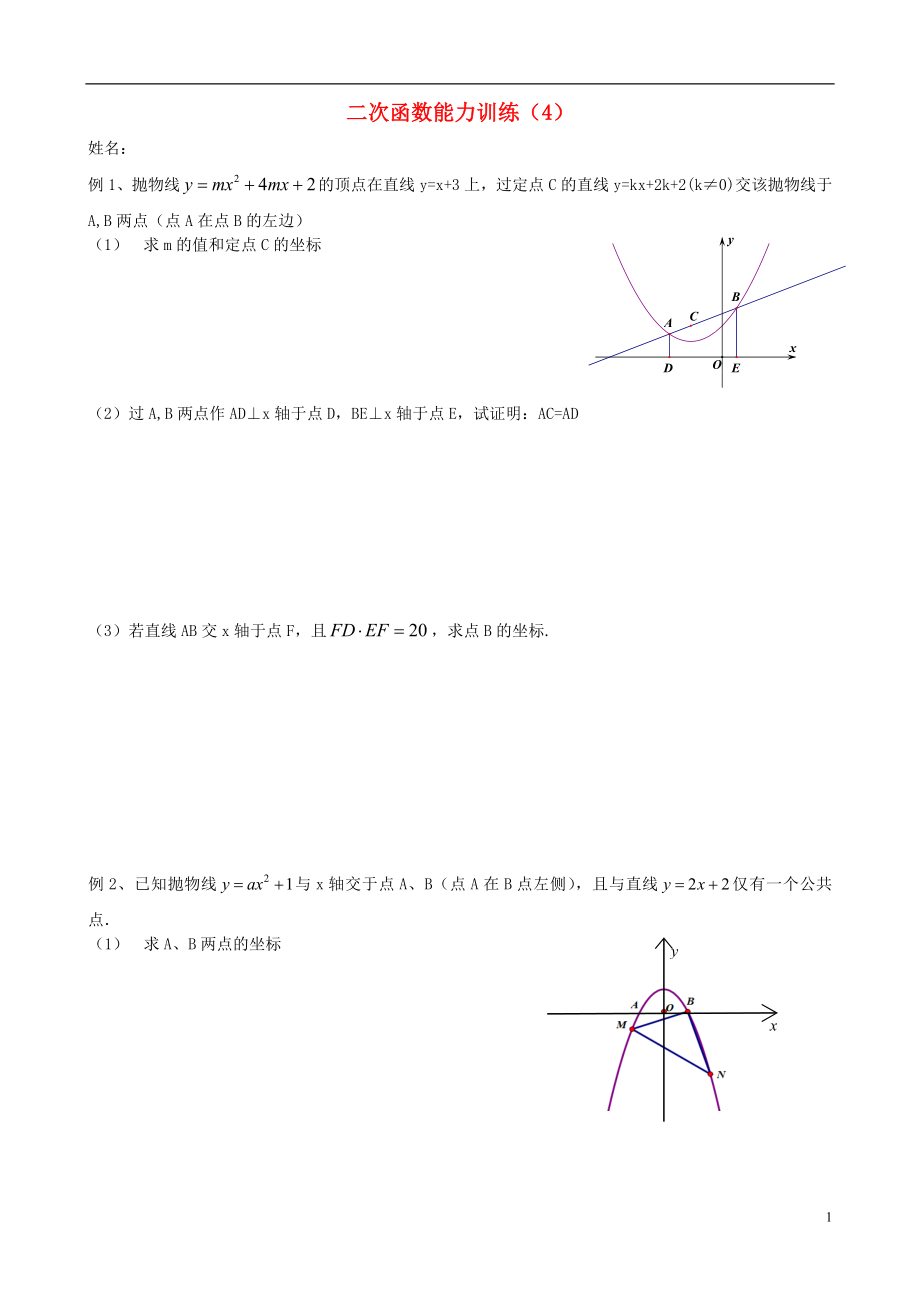
例1、拋物線的頂點(diǎn)在直線y=x+3上，過定點(diǎn)C的直線y=kx+2k+2(k≠0)交該拋物線于A,B兩點(diǎn)（點(diǎn)A在點(diǎn)B的左邊）
（1） 求m的值和定點(diǎn)C的坐標(biāo)
（2）過A,B兩點(diǎn)作AD⊥x軸于點(diǎn)D，BE⊥x軸于點(diǎn)E，試證明：AC=AD
（3）若直線AB交x軸于點(diǎn)F，且，求點(diǎn)B的坐標(biāo).
例2、已知拋物線與x軸交于點(diǎn)A、B（點(diǎn)A在B點(diǎn)左側(cè)），且與直線僅有一個(gè)公共點(diǎn)．
x
y
（1） 求A、B兩點(diǎn)的坐標(biāo)
（2）
2、如圖，作∠MBN=90°,交拋物線于M.N兩點(diǎn)，則直線MN必過定點(diǎn)Q,求點(diǎn)Q的坐標(biāo)．
例3、如圖，在平面直角坐標(biāo)系中，拋物線 y=ax2-2ax-3與x軸交于A、B，且AB=4，與y軸交于C點(diǎn)，
（1） 求拋物線的解析式
（3）若平行于直線AC的直線與拋物線交于M、N兩點(diǎn)，若拋物線上存在一個(gè)定點(diǎn)D，使過D點(diǎn)且平行于x軸的直線DE平分∠MDN，求D點(diǎn)坐標(biāo)
練習(xí)與作業(yè)
1、已知二次函數(shù)的圖象與x軸交于A,B兩點(diǎn)（A點(diǎn)在B點(diǎn)的左側(cè)
3、），與y軸負(fù)半軸交于點(diǎn)C，且AB=4，OB=OC.
（1）求二次函數(shù)的解析式；
（2）拋物線頂點(diǎn)為D，連接BC,BD，拋物線上是否存在點(diǎn)P使得∠PCB=∠CBD，若存在，求出點(diǎn)P的坐標(biāo)，若不存在，請(qǐng)說明理由.
2．已知拋物線C：y= +（2m﹣1）x﹣2m．
（1）若m=1，拋物線C交x軸于A，B兩點(diǎn)，求AB的長(zhǎng)；
（2） 若一次函數(shù)y=kx+mk的圖象與拋物線C有唯一公共點(diǎn)，求m的取值范圍；
（3）若m=2，M，N是拋物線C上兩動(dòng)點(diǎn)（點(diǎn)M在左，點(diǎn)N在右），分別過點(diǎn)M，N作PM∥x軸，PN∥y
4、軸，PM，PN交于點(diǎn)P，點(diǎn)M，N運(yùn)動(dòng)時(shí)，且始終保持MN=不變，當(dāng)△MNP得面積最大時(shí)，求直線MN的解析式．
3、如圖，拋物線與x軸交于A,B，與y軸交于C，連AC、BC，∠ABC=∠ACO.
（1）求拋物線的解析式
（2） 設(shè)P為線段OB上一點(diǎn)，過P作PN∥BC交OC于N，設(shè)直線PN：y=kx+m，將△PON沿PN折疊，得△PNM，點(diǎn)M恰好落在第四象限的拋物線上，求m的值
（3）CE平分∠ACB交拋物線的對(duì)稱軸于E，連AE，在拋物線上是否存在點(diǎn)P，使∠APC＞∠AEC，若存在，求出點(diǎn)P的橫坐標(biāo)的取值范圍，若不存在，請(qǐng)說明理由.
4
2018中考數(shù)學(xué)專題復(fù)習(xí) 二次函數(shù)能力訓(xùn)練（4）（無(wú)答案）
