山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 隨堂演練 第四章 幾何初步與三角形 第三節(jié) 等腰三角形與直角三角形試題

《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 隨堂演練 第四章 幾何初步與三角形 第三節(jié) 等腰三角形與直角三角形試題》由會(huì)員分享，可在線閱讀，更多相關(guān)《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 隨堂演練 第四章 幾何初步與三角形 第三節(jié) 等腰三角形與直角三角形試題（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

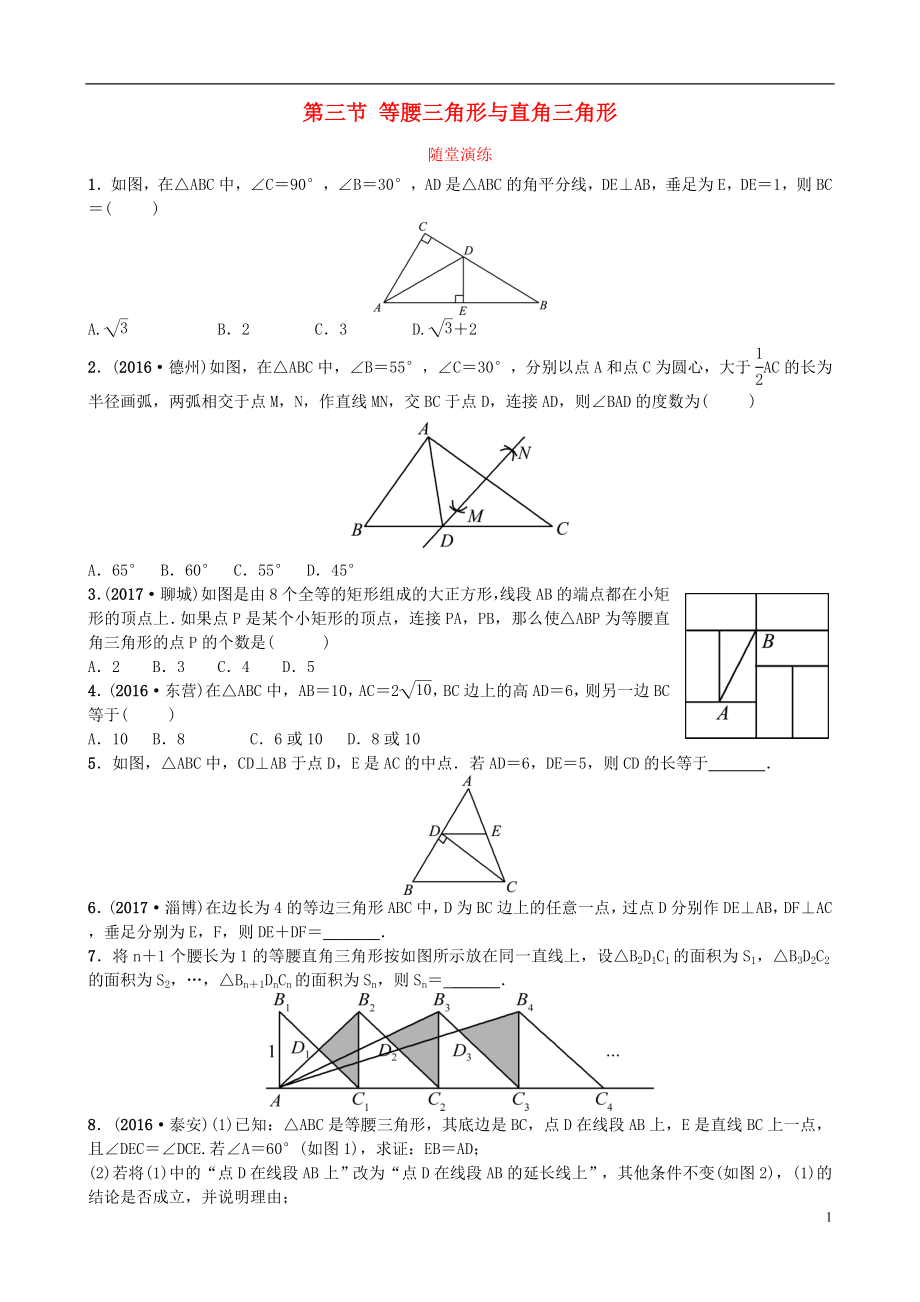
1、 第三節(jié) 等腰三角形與直角三角形 隨堂演練 1．如圖，在△ABC中，∠C＝90°，∠B＝30°，AD是△ABC的角平分線，DE⊥AB，垂足為E，DE＝1，則BC＝( ) A. B．2 C．3 D.＋2 2．(2016·德州)如圖，在△ABC中，∠B＝55°，∠C＝30°，分別以點(diǎn)A和點(diǎn)C為圓心，大于AC的長(zhǎng)為半徑畫(huà)弧，兩弧相交于點(diǎn)M，N，作直線MN，交BC于點(diǎn)D，連接AD，則∠BAD的度數(shù)為( ) A．65° B．60° C．55° D．45° 3．(2017·聊城)如圖是由8個(gè)全等的矩形組成的大正方形，線段AB的端點(diǎn)都在小矩形的頂點(diǎn)

2、上．如果點(diǎn)P是某個(gè)小矩形的頂點(diǎn)，連接PA，PB，那么使△ABP為等腰直角三角形的點(diǎn)P的個(gè)數(shù)是( ) A．2 B．3 C．4 D．5 4．(2016·東營(yíng))在△ABC中，AB＝10，AC＝2，BC邊上的高AD＝6，則另一邊BC等于( ) A．10 B．8 C．6或10 D．8或10 5．如圖，△ABC中，CD⊥AB于點(diǎn)D，E是AC的中點(diǎn)．若AD＝6，DE＝5，則CD的長(zhǎng)等于_______． 6．(2017·淄博)在邊長(zhǎng)為4的等邊三角形ABC中，D為BC邊上的任意一點(diǎn)，過(guò)點(diǎn)D分別作DE⊥AB，DF⊥AC，垂足分別為E，F(xiàn)，則DE＋DF＝____

3、___． 7．將n＋1個(gè)腰長(zhǎng)為1的等腰直角三角形按如圖所示放在同一直線上，設(shè)△B2D1C1的面積為S1，△B3D2C2的面積為S2，…，△Bn＋1DnCn的面積為Sn，則Sn＝ ______． 8．(2016·泰安)(1)已知：△ABC是等腰三角形，其底邊是BC，點(diǎn)D在線段AB上，E是直線BC上一點(diǎn)，且∠DEC＝∠DCE.若∠A＝60°(如圖1)，求證：EB＝AD； (2)若將(1)中的“點(diǎn)D在線段AB上”改為“點(diǎn)D在線段AB的延長(zhǎng)線上”，其他條件不變(如圖2)，(1)的結(jié)論是否成立，并說(shuō)明理由； (3)若將(1)中的“若∠A＝60°”改為“若∠A＝90°”，其他條件不變，則的值是

4、多少？(直接寫(xiě)出結(jié)論，不要求寫(xiě)解答過(guò)程) 參考答案 1．C　2.A　3.B　4.C 5．8　6.2　7. 8．(1)證明：如圖，過(guò)D點(diǎn)作DF∥BC交AC于點(diǎn)F，則AD＝DF. ∴∠FDC＝∠ECD. ∵∠DEC＝∠ECD，∴∠FDC＝∠DEC，ED＝CD. ∵∠DBE＝∠DFC＝120°，∴△DBE≌△CFD， ∴EB＝DF，∴EB＝AD. (2)解：EB＝AD成立．理由如下： 過(guò)點(diǎn)D作DF∥BC交AC的延長(zhǎng)線于點(diǎn)F， 則AD＝DF，∠FDC＝∠ECD. ∵∠DEC＝∠ECD， ∴∠FDC＝∠DEC，ED＝CD. ∵∠DBE＝∠DFC＝60°， ∴△DBE≌△CFD， ∴EB＝DF，∴EB＝AD. (3)＝. 2