《陜西省山陽(yáng)縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第21講 與圓有關(guān)的位置關(guān)系》由會(huì)員分享，可在線閱讀，更多相關(guān)《陜西省山陽(yáng)縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第21講 與圓有關(guān)的位置關(guān)系（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、第21講 與圓有關(guān)的位置關(guān)系
一、 知識(shí)清單梳理
知識(shí)點(diǎn)一：與圓有關(guān)的位置關(guān)系
關(guān)鍵點(diǎn)撥及對(duì)應(yīng)舉例
1.點(diǎn)與圓的位置關(guān)系
設(shè)點(diǎn)到圓心的距離為d.
(1) ?點(diǎn)在⊙O內(nèi)；(2) ?點(diǎn)在⊙O上；(3) ?點(diǎn)在⊙O外．
判斷點(diǎn)與圓之間的位置關(guān)系，將該點(diǎn)的圓心距與半徑作比較即可.
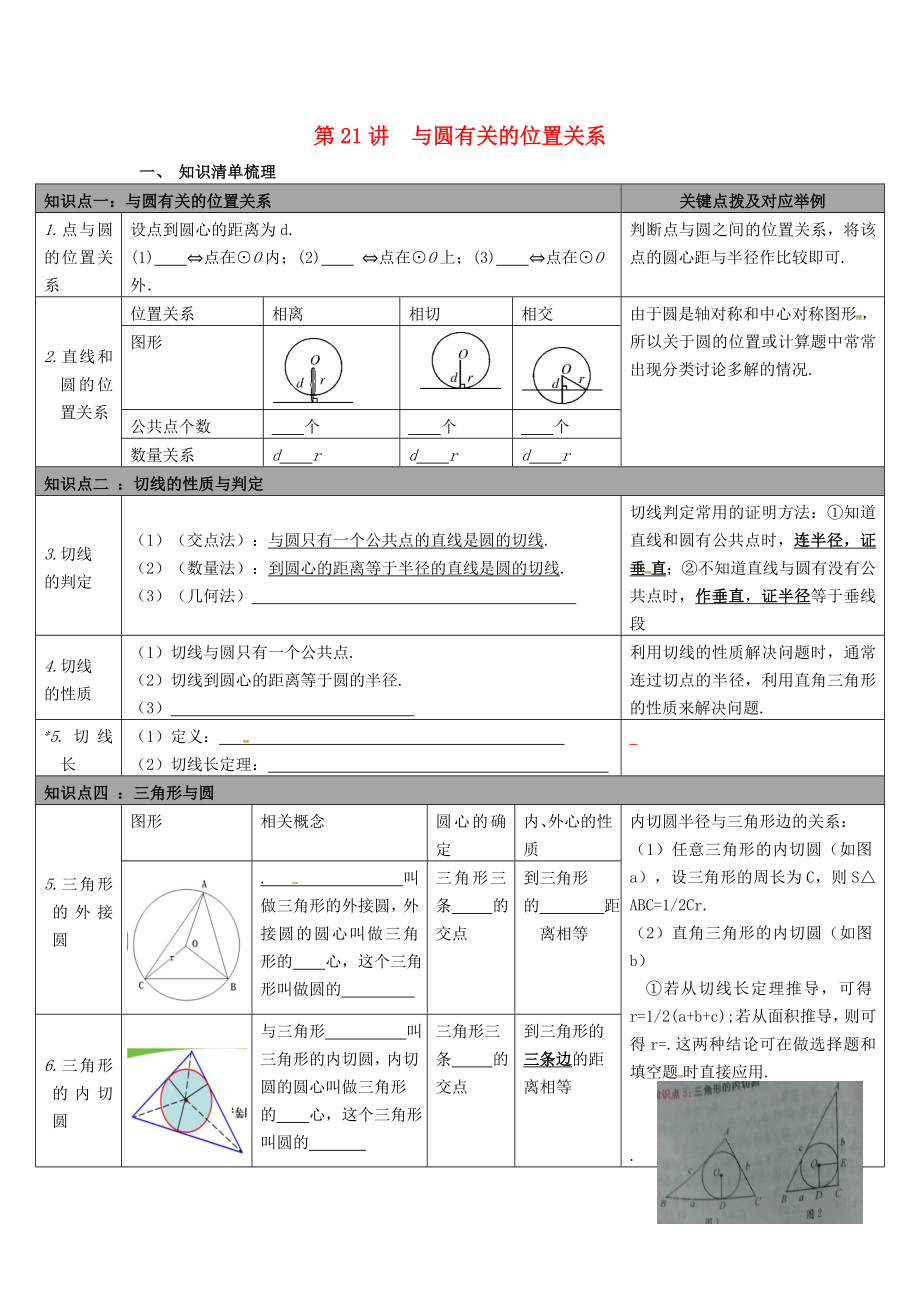
2.直線和圓的位置關(guān)系
位置關(guān)系
相離
相切
相交
由于圓是軸對(duì)稱和中心對(duì)稱圖形，所以關(guān)于圓的位置或計(jì)算題中常常出現(xiàn)分類討論多解的情況.
圖形
公共點(diǎn)個(gè)數(shù)
個(gè)
個(gè)
個(gè)
數(shù)量關(guān)系
d r
2、
d r
d r
知識(shí)點(diǎn)二 ：切線的性質(zhì)與判定
3.切線
的判定
（1）（交點(diǎn)法）：與圓只有一個(gè)公共點(diǎn)的直線是圓的切線.
（2）（數(shù)量法）：到圓心的距離等于半徑的直線是圓的切線.
（3）（幾何法）
切線判定常用的證明方法：①知道直線和圓有公共點(diǎn)時(shí)，連半徑，證垂直；②不知道直線與圓有沒(méi)有公共點(diǎn)時(shí)，作垂直，證半徑等于垂線段
4.切線
的性質(zhì)
（1）切線與圓只有一個(gè)公共點(diǎn).
（2）切線到圓心的距離等于圓的半徑.
（3）
3、
利用切線的性質(zhì)解決問(wèn)題時(shí)，通常連過(guò)切點(diǎn)的半徑，利用直角三角形的性質(zhì)來(lái)解決問(wèn)題.
*5.切線長(zhǎng)
（1）定義：
（2）切線長(zhǎng)定理：
知識(shí)點(diǎn)四 ：三角形與圓
5.三角形的外接圓
圖形
相關(guān)概念
圓心的確定
內(nèi)、外心的性質(zhì)
內(nèi)切圓半徑與三角形邊的關(guān)系：
（1）任意三角形的內(nèi)切圓（如圖a），設(shè)三角形的周長(zhǎng)為C，則S△ABC=1/2Cr.
（2）直角三角形的內(nèi)切圓（如圖b）
①若從切線長(zhǎng)定理推導(dǎo)，可得r
4、=1/2(a+b+c);若從面積推導(dǎo)，則可得r=.這兩種結(jié)論可在做選擇題和填空題時(shí)直接應(yīng)用.
.
. 叫做三角形的外接圓，外接圓的圓心叫做三角形的 心，這個(gè)三角形叫做圓的
三角形三條 的交點(diǎn)
到三角形
的 距離相等
6.三角形的內(nèi)切圓
與三角形 叫三角形的內(nèi)切圓，內(nèi)切圓的圓心叫做三角形的 心，這個(gè)三角形叫圓的
三角形三條 的交點(diǎn)
到三角形的三條邊的距離相等
二、 例題試做：
例1：已知：⊙O的半徑為2，圓心到直線l的距離為1，將直線l沿垂直于l的方向平移，使l與⊙O相切，則平移的距離是 .
例2：如圖，AB、AC、DB是⊙O的切線，P、C、D為切點(diǎn)，
如果AB=5，AC=3，則BD的長(zhǎng)為
例3：已知△ABC的三邊長(zhǎng)a=3，b=4，c=5，則它的外切圓半徑是 .
三、 課后練習(xí)：
內(nèi)參：選擇題：13、14、16
填空題：6、7、13
解答題：1
陜西真題：3、4（在錯(cuò)題收集本上完成，要求抄題畫圖，兩題之間留空批改）
陜西省山陽(yáng)縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第21講 與圓有關(guān)的位置關(guān)系
