《備戰(zhàn)2022 中考數(shù)學(xué) 一輪復(fù)習(xí) 素養(yǎng)綜合練測26 多邊形和平行四邊形（教師版）》由會員分享，可在線閱讀，更多相關(guān)《備戰(zhàn)2022 中考數(shù)學(xué) 一輪復(fù)習(xí) 素養(yǎng)綜合練測26 多邊形和平行四邊形（教師版）（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、
素養(yǎng)綜合練測26 多邊形和平行四邊形
(時間：45分鐘)
題號
1
2
3
4
5
6
答案
C
D
C
C
C
B
1.(2021·云南)一個十邊形的內(nèi)角和等于( C )
A．1800° B．1660° C．1440° D．1200°
2．(2021·眉山)正八邊形中，每個內(nèi)角與每個外角的度數(shù)之比為( D )
A．1∶3 B．1∶2 C．2∶1 D．3∶1
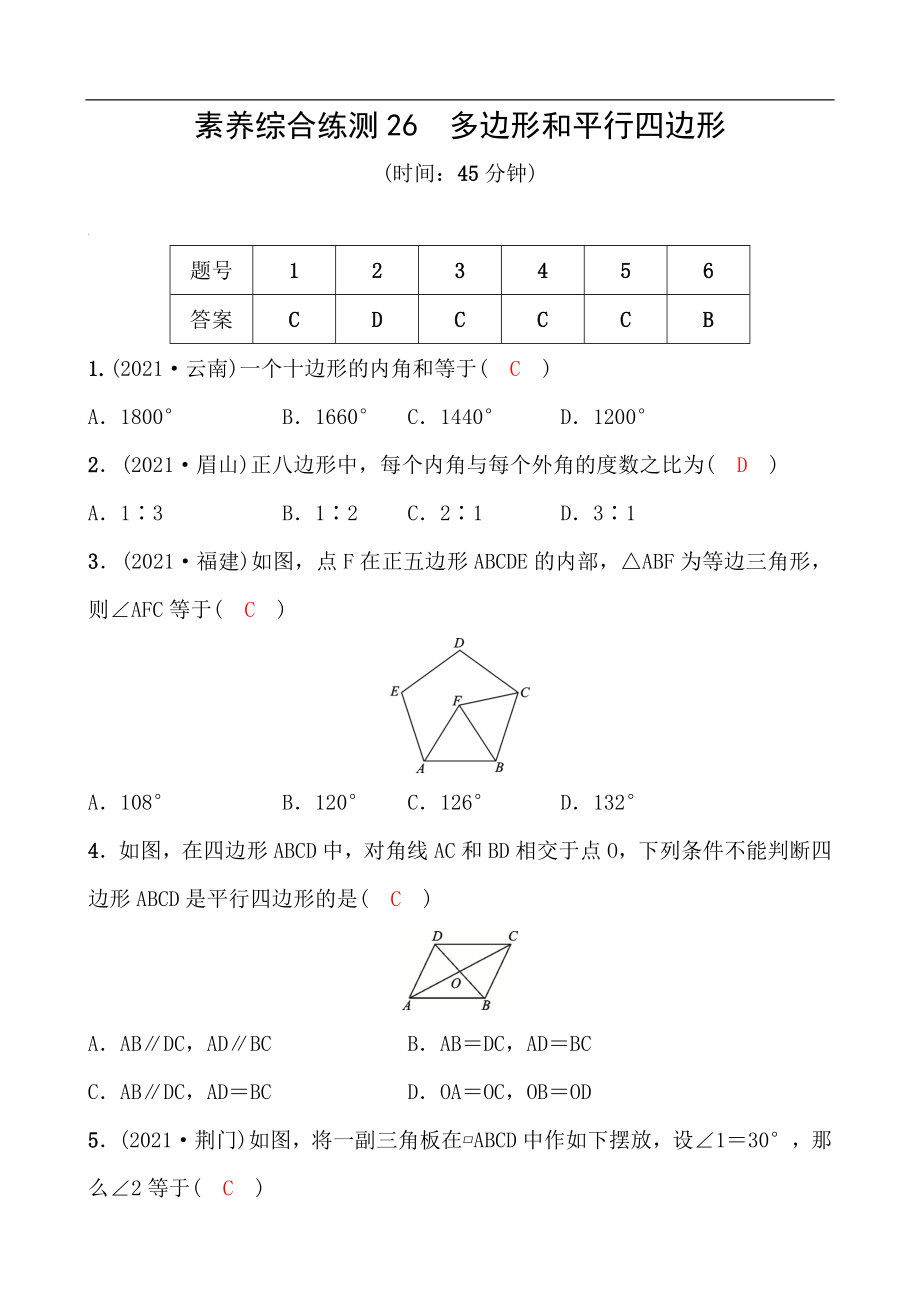
3．(2021·福建)如圖，點(diǎn)F在正五邊形ABCDE的內(nèi)部，△ABF為等邊三角形，則∠AFC等于( C )
A．108° B．120° C．126° D．132°
4．如圖，
2、在四邊形ABCD中，對角線AC和BD相交于點(diǎn)O，下列條件不能判斷四邊形ABCD是平行四邊形的是( C )
A．AB∥DC，AD∥BC B．AB＝DC，AD＝BC
C．AB∥DC，AD＝BC D．OA＝OC，OB＝OD
5．(2021·荊門)如圖，將一副三角板在?ABCD中作如下擺放，設(shè)∠1＝30°，那么∠2等于( C )
A．55° B．65° C．75° D．85°
6．(2021·蘇州)如圖，在平行四邊形ABCD中，將△ABC沿著AC所在的直線折疊得到△AB′C，B′C交AD于點(diǎn)E，連結(jié)B′D，若∠B＝60°，∠ACB＝45°，AC＝，則B′D的長是( B )
3、A．1 B. C. D.
7．如果一個正方形被截掉一個角后，得到一個多邊形，那么這個多邊形的內(nèi)角和是 540°或360°或180° ．
8．(2021·湘潭)如圖，在?ABCD中，對角線AC，BD相交于點(diǎn)O，點(diǎn)E是邊AB的中點(diǎn)．已知BC＝10，則OE＝ 5 ．
9．(2021·常州)如圖，在平面直角坐標(biāo)系xOy中，四邊形OABC是平行四邊形，其中點(diǎn)A在x軸正半軸上．若BC＝3，則點(diǎn)A的坐標(biāo)是 (3，0) ．
10．如圖，在?ABCD中，E，F(xiàn)是對角線AC上兩點(diǎn)，AE＝EF＝CD，∠ADF＝90°，∠BCD＝63°，則∠ADE的大小為 21 °.
11．如圖，在平行四邊形A
4、BCD中，連結(jié)BD，且BD＝CD，過點(diǎn)A作AM⊥BD于點(diǎn)M，過點(diǎn)D作DN⊥AB于點(diǎn)N，且DN＝3，在DB的延長線上取一點(diǎn)P，滿足∠ABD＝∠MAP＋∠PAB，則AP＝ 6 ．
12．(2021·江西)如圖，將?ABCD沿對角線AC翻折，點(diǎn)B落在點(diǎn)E處，CE交AD于點(diǎn)F，若∠B＝80°，∠ACE＝2∠ECD，F(xiàn)C＝a，F(xiàn)D＝b，則?ABCD的周長為 4a＋2b ．
13．(2018·衢州)如圖，在?ABCD中，AC是對角線，BE⊥AC，DF⊥AC，垂足分別為點(diǎn)E，F(xiàn)，求證：AE＝CF.
證明：∵四邊形ABCD是平行四邊形，
∴AB＝CD，AB∥CD.
∴∠BAE＝∠DCF.
5、
又BE⊥AC，DF⊥AC，
∴∠AEB＝∠CFD＝90°.
在△ABE和△CDF中，
∴△ABE≌△CDF(AAS)．∴AE＝CF.
14．(2021·岳陽)如圖，在四邊形ABCD中，AE⊥BD，CF⊥BD，垂足分別為點(diǎn)E，F(xiàn).
(1)請你只添加一個條件(不另加輔助線)，使得四邊形AECF為平行四邊形，你添加的條件是 AE＝CF ；
(2)添加了條件后，證明四邊形AECF為平行四邊形．
(1)解：AE＝CF(答案不唯一)
(2)證明：∵AE⊥BD，CF⊥BD，
∴AE∥CF.
又AE＝CF，
∴四邊形AECF為平行四邊形．
15．如圖，在△ABC中，∠ACB＝9
6、0°，∠CAB＝30°，以線段AB為邊向外作等邊△ABD，點(diǎn)E是線段AB的中點(diǎn)，
連結(jié)CE并延長交線段AD于點(diǎn)F.
(1)求證：四邊形BCFD為平行四邊形；
(2)若AB＝6，求?BCFD的面積．
(1)證明：在△ABC中，
∠ACB＝90°，∠CAB＝30°，
∴∠ABC＝60°.
在等邊三角形ABD中，∠BAD＝60°，
∴∠BAD＝∠ABC＝60°.
∵E為AB的中點(diǎn)，∴AE＝BE.
在△AEF和△BEC中，
∴△AEF≌△BEC(ASA)．∴∠AFE＝∠BCE.
在△ABC中，∠ACB＝90°，E為AB的中點(diǎn)，
∴CE＝AB，BE＝AB.
∴CE＝A
7、E.∴∠EAC＝∠ECA＝30°.
∴∠BCE＝∠EBC＝60°.∴∠AFE＝60°.
又∠D＝60°，∴FC∥BD.
又∠BAD＝∠ABC＝60°，
∴AD∥BC，即FD∥BC.
∴四邊形BCFD是平行四邊形．
(2)解：在Rt△ABC中，∵∠BAC＝30°，AB＝6，
∴BC＝AB＝3，AC＝BC＝3.
∴S?BCFD＝3×3＝9.
16．(2021·龍東)如圖，平行四邊形ABFC的對角線AF，BC相交于點(diǎn)E，點(diǎn)O為AC的中點(diǎn)，連結(jié)BO并延長，交FC的延長線于點(diǎn)D，交AF于點(diǎn)G，連結(jié)AD，OE，若平行四邊形ABFC的面積為48，則△AOG的面積為( C )
8、A．5.5 B．5 C．4 D．3
17．(2021·寧波模擬)如圖，已知E，F(xiàn)為?ABCD對角線AC上兩點(diǎn)，且AE＝CF，過E，F(xiàn)將?ABCD分制成9個小的平行四邊形，則已知下列哪個選項中的圖形面積，就可以求出△GIN的面積( C )
A．△AHF B．△GHN
C．四邊形AHPI D．四邊形IPFJ
18．(2021·廣元)如圖，在平行四邊形ABCD中，E為DC邊的中點(diǎn)，連結(jié)AE，若AE的延長線和BC的延長線相交于點(diǎn)F.
(1)求證：BC＝CF；
(2)連結(jié)AC和BE相交于點(diǎn)G，若△GEC的面積為2，求平行四邊形ABCD的面積．
(1)證明：∵四邊形ABCD是平行四邊形，
∴AD∥BC，AD＝BC.∴∠D＝∠FCE.
∵E為DC的中點(diǎn)，∴ED＝EC.
在△ADE和△FCE中，
∴△ADE≌△FCE(ASA)．
∴AD＝FC.
∴BC＝CF.
(2)解：∵四邊形ABCD是平行四邊形，
∴AB∥CD，AB＝CD.
∴△ABG∽△CEG.
∴＝，＝.
∵DE＝CE，∴AB＝2CE.
∴＝2，＝4.
∵△GEC的面積為2，
∴S△BGC＝2S△CEG＝4，S△ABG＝4S△CEG＝8.
∴S△ABC＝S△BGC＋S△ABG＝4＋8＝12.
∴平行四邊形ABCD的面積為2S△ABC＝24.
備戰(zhàn)2022 中考數(shù)學(xué) 一輪復(fù)習(xí) 素養(yǎng)綜合練測26 多邊形和平行四邊形（教師版）
