《【優(yōu)化設(shè)計】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 單元檢測五》由會員分享���,可在線閱讀����,更多相關(guān)《【優(yōu)化設(shè)計】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 單元檢測五(10頁珍藏版)》請在裝配圖網(wǎng)上搜索��。
1�����、
四邊形
(時間:90分鐘 總分:120分)
一、選擇題(每小題4分,共40分)
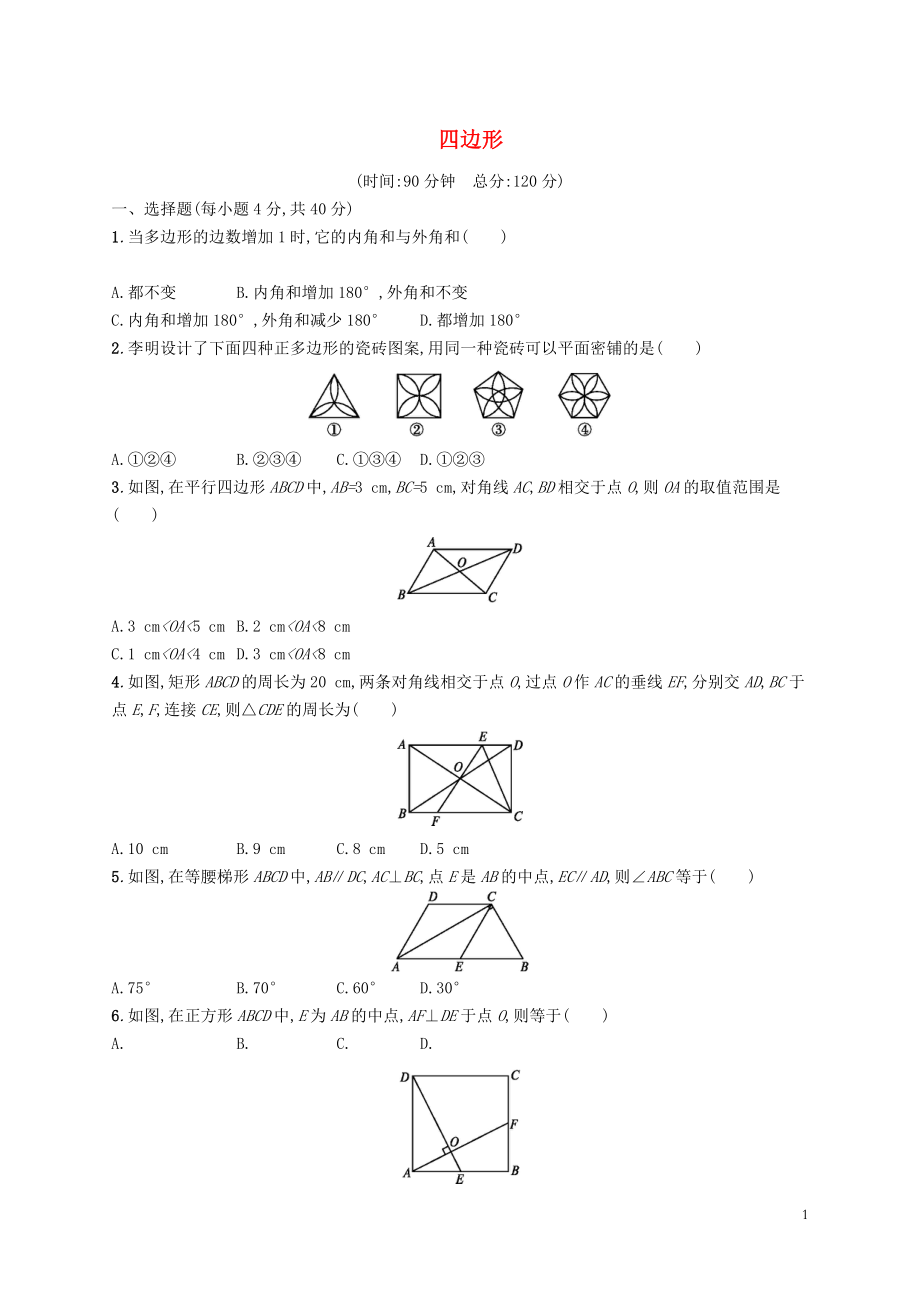
1.當(dāng)多邊形的邊數(shù)增加1時,它的內(nèi)角和與外角和( )
A.都不變 B.內(nèi)角和增加180°,外角和不變
C.內(nèi)角和增加180°,外角和減少180° D.都增加180°
2.李明設(shè)計了下面四種正多邊形的瓷磚圖案,用同一種瓷磚可以平面密鋪的是( )
A.①②④ B.②③④ C.①③④ D.①②③
3.如圖,在平行四邊形ABCD中,AB=3 cm,BC=5 cm,對角線AC,BD相交于點O,則OA的取值范圍是( )
A.3
2��、cm
3��、. D.
7.如圖,在菱形ABCD中,∠B=60°,AB=2,E,F分別是BC,CD的中點,連接AE,EF,AF,則△AEF的周長為( )
A.2 B.3 C.4 D.3
8.如圖,菱形ABCD由6個腰長為2,且全等的等腰梯形鑲嵌而成,則線段AC的長為( )
A.3 B.6 C.3 D.6
9.如圖,邊長為6的大正方形中有兩個小正方形,若兩個小正方形的面積分別為S1,S2,則S1+S2的值為( )
A.16 B.17 C.18 D.19
10.正方形ABCD�����、正方形BEFG和正方形RKPF的位置如圖所示,點G在線段DK上,正方形BEFG的邊長為4,則△D
4����、EK的面積為( )
A.10 B.12 C.14 D.16
二、填空題(每小題4分,共24分)
11.如圖,在四邊形ABCD中,對角線AC,BD交于點O,OA=OC,OB=OD,添加一個條件使四邊形ABCD是菱形,那么所添加的條件可以是 (寫出一個即可).?
12.已知正六邊形的邊長為1 cm,分別以它的三個不相鄰的頂點為圓心,1 cm長為半徑畫弧(如圖),則所得到的三條弧的長度之和為 cm.(結(jié)果保留π)?
13.如圖所示,兩個全等菱形的邊長為1米,一個微型機器人由A點開始按ABCDEFCGA的順序沿菱形的邊循環(huán)運動,行走2 015米停下,則這個微
5�����、型機器人停在點 .?
14.如圖,邊長為1的兩個正方形互相重合,按住其中一個不動,將另一個繞頂點A順時針旋轉(zhuǎn)45°,則這兩個正方形重疊部分的面積是 .?
15.如圖,在梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分別以DA,AB,BC為邊向梯形外作正方形,其面積分別為S1,S2,S3,則S1,S2,S3之間的關(guān)系是 .?
16.如圖,在邊長為2 cm的正方形ABCD中,點Q為BC邊的中點,點P為對角線AC上一動點,連接PB,PQ,則△PBQ周長的最小值為 cm.(結(jié)果不取近似值)?
三����、解答題(56分)
6、
17.(6分)已知,如圖,E,F是四邊形ABCD的對角線AC上的兩點,AF=CE,DF=BE,DF∥BE.
(1)求證:△AFD≌△CEB;
(2)四邊形ABCD是平行四邊形嗎?請說明理由.
18.(8分)如圖,在?ABCD中,E,F分別為邊AB,CD的中點,連接DE,BF,BD.
(1)求證:△ADE≌△CBF;
(2)若AD⊥BD,則四邊形BFDE是什么特殊四邊形?請證明你的結(jié)論.
19.(10分)如圖,分別以Rt△ABC的直角邊AC及斜邊AB向外作等邊△ACD��、等邊△ABE.已知∠BAC=30°,EF⊥AB,垂足為F,連接DF.
(1)
7���、試說明AC=EF;
(2)求證:四邊形ADFE是平行四邊形.
20.(10分)如圖,把正方形ABCD繞點C按順時針方向旋轉(zhuǎn)45°得到正方形A'B'CD'(此時,點B'落在對角線AC上,點A'落在CD的延長線上),A'B'交AD于點E,連接AA',CE.
求證:(1)△ADA'≌△CDE;
(2)直線CE是線段AA'的垂直平分線.
21.(10分)如圖,△ADC,△ABE,△BCF均為直線BC同側(cè)的等邊三角形.
(1)當(dāng)AB≠AC時,證明四邊形ADFE為平行四邊形;
(2)當(dāng)AB=AC時,順次連接A,D,F,E四點所構(gòu)成的圖形有哪幾類?直接寫出構(gòu)成圖形的類型和
8�����、相應(yīng)的條件.
22.(12分)如圖是小紅設(shè)計的鉆石形商標(biāo),△ABC是邊長為2的等邊三角形,四邊形ACDE是等腰梯形,AC∥ED,∠EAC=60°,AE=CD=1.
(1)求證:△ABE≌△CBD;
(2)圖中存在多對相似三角形,請你找出一對進(jìn)行證明,并求出其相似比(不添加輔助線,不找全等的相似三角形);
(3)小紅發(fā)現(xiàn)AM=MN=NC,請證明此結(jié)論;
(4)求線段BD的長.
##
一���、選擇題(每小題4分,共40分)
1.B 多邊形的外角和為360°,與邊數(shù)無關(guān);由內(nèi)角和公式(n-2)180°得n增加1,內(nèi)角和增加180°,故選B.
2.A ③是正五邊形,幾個正五邊形的內(nèi)
9����、角繞著一點不能拼成一個周角,所以正五邊形不可以密鋪.
3.C 在△ABC中,BC-AB
10、.D ∵E為AB的中點,
∴AE=AB.
∵四邊形ABCD是正方形,
∴AB=AD.∴AE=AD.
由△OAE∽△ODA得,
則.
7.B 由對稱性知,AE=AF.如圖,連接AC,由題意可得,AE,AF分別是等邊△ABC,△ADC頂角的平分線,
∴∠1=∠2=∠3=∠4=30°,
∴∠EAF=60°.∴△AEF是等邊三角形.
在Rt△ABE中,由勾股定理可得,AE=,
∴△AEF的周長為3,故選B.
8.D ∵菱形ABCD由6個腰長為2,且全等的等腰梯形鑲嵌而成,∴分析圖形可得,這個菱形的邊長為6,且較小的內(nèi)角為60°.連接AC,BD交于點O,則AC⊥BD,AC=2A
11����、O,∠CAB=∠DAB=30°.
在Rt△AOB中,∠CAB=30°,AB=6,
∴AO=ABcos∠CAB=6×=3.
∴AC=2AO=6.故選D.
9.B 如圖,由正方形的性質(zhì)可知,∠FAE=∠AFE=45°.
∴AE=EF.又∵EF=EB,
∴AE=EF=EB.
∴EF=AB=3.
∴S1=3×3=9.
設(shè)DN=x,則由勾股定理得MN=x.
∴NK=KC=MN=x.
由勾股定理得NC=NK=2x.
∴DC=DN+NC=3x.∴3x=6.∴x=2.
∴NK=x=2.∴S2=(2)2=8.
∴S1+S2=9+8=17.故選B.
10.D 設(shè)正方形ABCD的邊
12、長為a,正方形RKPF的邊長為c,可得S△DEK=S正方形ABCD+S正方形BEFG+S正方形RKPF+S△REK-S△DCG-S△GKP-S△ADE=a2+42+c2+c(4-c)-a(a-4)-c(4+c)-a(4+a)=a2+16+c2+2c-c2-a2+2a-2c-c2-2a-a2=16.故選D.
二���、填空題(每小題4分,共24分)
11.AB=AD(答案不唯一) ∵OA=OC,OB=OD,
∴四邊形ABCD是平行四邊形.
∵鄰邊相等的平行四邊形是菱形,
∴添加的條件可以是AB=AD(答案不唯一).
12.2π ∵正六邊形的內(nèi)角為120°,
∴每條弧的長度為圓周長的.
13��、
∴三條弧的長度之和為圓的周長,等于2π cm.
13.G 機器人從A點開始循環(huán)運動一次經(jīng)過9個點運動8米,而運動1米一個點,所以2 015÷8=251余7,即循環(huán)運動251次余7米,故到點G停止.
14.-1 在Rt△ABC中,∵AB=BC=1,∠CAB=45°,
∴AC=.
又∵AD'=1,∴CD'=-1.
在Rt△CD'E中,∵∠D'CE=45°,
∴CD'=D'E=-1.
∴這兩個正方形重疊部分的面積是
S△ABC-S△CD'E=×1×1-×(-1)2=-1.
15.S2=S1+S3 如圖,過點B作BE∥AD,交BC于點E,
則∠BEC=∠ADC.
∵∠AD
14��、C+∠BCD=90°,
∴∠BEC+∠BCD=90°.
∴△BEC為直角三角形.
∵其面積為S1,S2,S3的正方形的邊長為DA=,AB=,BC=,
又∵DC=2AB,AB=DE,DA=BE,
∴EC=,BE=.
在Rt△BEC中,BE2+BC2=EC2,
∴S2=S1+S3.
16.
(+1) 如圖,連接QD交AC于點P,連接BP,BD.
∵點D是點B關(guān)于直線AC的對稱點,而AC垂直平分BD,
∴PB=PD.∴PB+PQ=PD+PQ=QD最小.
在Rt△DCQ中,QC=1,DC=2,
∴QD=.
∴△PBQ周長的最小值為(+1)cm.
三����、解答題(56分)
15��、
17.解:(1)證明:∵DF∥BE,
∴∠DFA=∠BEC.
∵在△AFD和△CEB中,DF=BE,∠DFA=∠BEC,AF=CE,
∴△AFD≌△CEB(SAS).
(2)四邊形ABCD是平行四邊形,
理由如下:∵△AFD≌△CEB,
∴AD=CB,∠DAF=∠BCE.
∴AD∥CB.
∴四邊形ABCD是平行四邊形.
18.解:(1)證明:在?ABCD中,∠A=∠C,AD=CB,AB=CD,
∵E,F分別是AB,CD的中點,
∴AE=CF.在△AED和△CFB中,
∴△ADE≌△CBF(SAS).
(2)若AD⊥BD,則四邊形BFDE是菱形.
∵AD⊥BD,
16、∴△ABD是直角三角形,且AB是斜邊.
∵E是AB的中點,∴DE=AB=BE.
由題意知EB∥DF,且EB=DF,
∴四邊形BFDE是平行四邊形.
∵DE=BE,∴四邊形BFDE是菱形.
19.解:(1)∵△ABE是等邊三角形,FE⊥AB于點F,
∴∠AEF=30°,AB=AE,∠EFA=90°.
在Rt△AEF和Rt△BAC中,
∴△AEF≌△BAC(AAS).∴AC=EF.
(2)∵△ACD是等邊三角形,
∴∠DAC=60°,AC=AD.
∴∠DAB=60°+30°=90°.
又EF⊥AB,∴∠EFA=90°=∠DAB.
∴AD∥EF.
又∵AC=EF(已證
17��、),AC=AD,
∴AD=EF.∴四邊形ADFE是平行四邊形.
20.解:證明:(1)∵四邊形ABCD是正方形,
∴AD=CD,∠ADC=90°.
∴∠A'DE=90°,
根據(jù)旋轉(zhuǎn)的方法可得,∠EA'D=45°.
∴∠A'ED=45°.∴A'D=DE.
在△AA'D和△CED中,
∴△AA'D≌△CED.
(2)∵AC=A'C,
∴點C在AA'的垂直平分線上.
∵AC是正方形ABCD的對角線,
∴∠CAE=45°.
∵AC=A'C,CD=CB',
∴AB'=A'D.
在△AEB'和△A'ED中,
∴△AEB'≌△A'ED,∴AE=A'E.
∴點E也在AA'的垂
18����、直平分線上.
∴直線CE是線段AA'的垂直平分線.
21.解:(1)證明:∵△ABE,△BCF為等邊三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.∴∠FBE=∠CBA.
∴△FBE≌△CBA.
∴EF=AC.
又△ADC為等邊三角形,
∴CD=AD=AC.∴EF=AD.
同理可得AE=DF.
∴四邊形AEFD是平行四邊形.
(2)構(gòu)成的圖形有兩類,一類是菱形,一類是線段.
當(dāng)圖形為菱形時,∠BAC≠60°(或A與F不重合、△ABC不為正三角形);
當(dāng)圖形為線段時,∠BAC=60°(或A與F重合�����、△ABC為正三角形).
22.解:(1)證明
19���、:∵△ABC是等邊三角形,
∴AB=BC,∠BAC=∠BCA=60°.
∵四邊形ACDE是等腰梯形,∠EAC=60°,
∴∠ACD=∠CAE=60°.
∴∠BAC+∠CAE=120°=∠BCA+∠ACD,
即∠BAE=∠BCD.
在△ABE和△CBD中,
∴△ABE≌△CBD.
(2)答案不唯一.如△ABN∽△CDN.
∵∠BAN=60°=∠DCN,∠ANB=∠DNC,
∴△ANB∽△CND.
其相似比為=2.
(3)由(2)得=2,
∴CN=AN=AC.
同理AM=AC.∴AM=MN=NC.
(4)如圖,作DF⊥BC交BC的延長線于點F,
∵∠BCD=120°,
∴∠DCF=60°.
在Rt△CDF中,
∴∠CDF=30°.
∴CF=CD=.
∴DF=.
在Rt△BDF中,BF=BC+CF=2+,DF=,
∴BD=.
10
 【優(yōu)化設(shè)計】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 單元檢測五
【優(yōu)化設(shè)計】(福建專版)2015中考數(shù)學(xué)總復(fù)習(xí) 單元檢測五