《《多邊形的內(nèi)角和與外角和》教學(xué)設(shè)計(jì)-04》由會(huì)員分享�,可在線閱讀,更多相關(guān)《《多邊形的內(nèi)角和與外角和》教學(xué)設(shè)計(jì)-04(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1�、《多邊形的內(nèi)角和與外角和》教學(xué)設(shè)計(jì)
教學(xué)目標(biāo):
1 了解多邊形的外角和的概念、掌握多邊形的外角和公式����。
2 了解正多邊形的概念。
3 了解四邊形的不穩(wěn)定性及生活中的運(yùn)用�。
4通過(guò)多邊形內(nèi)角和的探索,讓學(xué)生體驗(yàn)從特殊到一般的思考方法�����。
重點(diǎn)��、難點(diǎn):
重點(diǎn):多邊形的外角的概念����、多邊形的外角和公式。
難點(diǎn):多邊形外角和公式的推導(dǎo)過(guò)程�����。
教學(xué)過(guò)程:
一創(chuàng)設(shè)情境�,導(dǎo)入新課
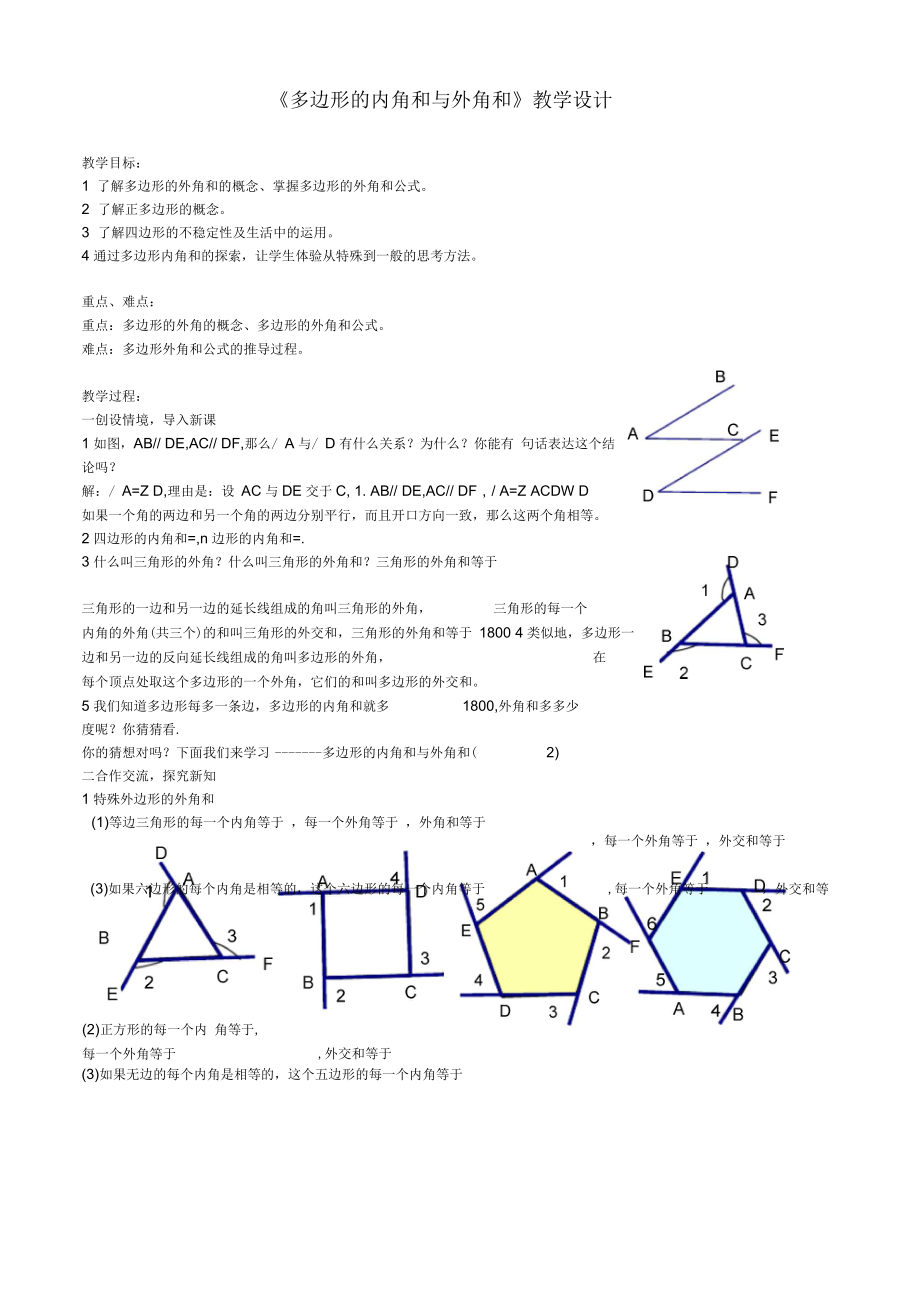
1如圖,AB// DE,AC// DF,那么/ A與/ D有什么關(guān)系�?為什么����?你能有 句話表達(dá)這個(gè)結(jié)論嗎���?
解:/ A=Z D,理由是:設(shè) AC與DE交于C, 1. AB// DE,AC// DF�����,/ A=Z
2���、ACDW D
如果一個(gè)角的兩邊和另一個(gè)角的兩邊分別平行,而且開(kāi)口方向一致�����,那么這兩個(gè)角相等����。
2四邊形的內(nèi)角和=,n邊形的內(nèi)角和=.
3什么叫三角形的外角���?什么叫三角形的外角和�?三角形的外角和等于
三角形的一邊和另一邊的延長(zhǎng)線組成的角叫三角形的外角���, 三角形的每一個(gè)
內(nèi)角的外角(共三個(gè))的和叫三角形的外交和�,三角形的外角和等于 1800 4類似地,多邊形一邊和另一邊的反向延長(zhǎng)線組成的角叫多邊形的外角���, 在
每個(gè)頂點(diǎn)處取這個(gè)多邊形的一個(gè)外角��,它們的和叫多邊形的外交和�����。
5我們知道多邊形每多一條邊����,多邊形的內(nèi)角和就多 1800,外角和多多少
度呢����?你猜猜看.
你的猜想對(duì)嗎?下面我
3���、們來(lái)學(xué)習(xí) 多邊形的內(nèi)角和與外角和( 2)
二合作交流����,探究新知
1特殊外邊形的外角和
(1)等邊三角形的每一個(gè)內(nèi)角等于 ��,每一個(gè)外角等于 ,外角和等于
(2)正方形的每一個(gè)內(nèi) 角等于,每一個(gè)外角等于
,外交和等于
�,每一個(gè)外角等于 ,外交和等于
(3)如果六邊形的每個(gè)內(nèi)角是相等的����,這個(gè)六邊形的每一個(gè)內(nèi)角等于
,每一個(gè)外角等于
,外交和等
(3)如果無(wú)邊的每個(gè)內(nèi)角是相等的����,這個(gè)五邊形的每一個(gè)內(nèi)角等于
求?
量 P
個(gè)內(nèi)角
(交
/ 1 + Z
畫(huà) OD//
從上面的多邊形看到��,邊數(shù)增加����,外角和并沒(méi)有增加,都是 360 o,但這些多邊形的是特殊的����,是
4�����、否任意的
多邊形內(nèi)角和都等于等于 360��。呢? 2普通多邊形的外角和
(1)四邊形的外角和
如圖�,四邊形 ABCD的四個(gè)外角/ 1+/2+/3+/4=?用什么方法來(lái) 方法1量出這4個(gè)角的度數(shù),然后相加��,看等于多少����?請(qǐng)你量一 113圖3—87中的四個(gè)外角。
方法2我們知道四邊形的四個(gè)內(nèi)角的和是 360 o,四個(gè)外角與四
有什么關(guān)系呢���?為了表達(dá)方便���,我們把四個(gè)內(nèi)角也用數(shù)字表示。
流)�����,估計(jì)學(xué)生會(huì)想到:
? ??/ 1 + Z 5=180 o, / 2+Z 6=180 o, / 3+Z 7=180 o
/ 4+/ 8=180 o
? ?/ 1=180o-/5, /2=180o-/6
5��、, /3=180o-/7, /4=180o-/8, 2+Z 3+Z4=4x180o- (Z 5+Z6+Z7+Z8) =4x180 o-360 o=360o 方法 3 :畫(huà) OA/ BC,OB// AB,則/ 2=/AOB,畫(huà) OC/ AD,則 / 1 = / BOC, CD,則/ 4=/ COD/ 3=Z AOD,
? ??/ AOB吆 / BOC吆 COD廿 AOD=36o,
? ??/ 1 + Z 2+Z 3+Z 4=360o.
(2) n邊形的外角和等于多少呢����?(交流討論)
??? n邊形的每一個(gè)外角與它相鄰的內(nèi)角的和是
n邊形的內(nèi)角和加外角和等于
??? n邊形的內(nèi)角和
6、等于
n 邊形的外角和等于 n ? 180o - (n- 2) ? 180o =360o
歸納:n邊形的外角和等于 360o 3正多邊形的概念
觀察下面多邊形���,它們的角和邊有什么特點(diǎn)����?(邊都相等,角也都相等)
多邊形�����。
定相等嗎�����?
中間一個(gè)的四
變��,但形狀可以
在平面內(nèi)���,邊都相等�、角也都相等的多邊形叫正
4四邊形的不穩(wěn)定性
動(dòng)腦筋:
四條邊都相等的四邊形(即菱形)它的四個(gè)角一 觀察下面菱形�,它們的四條邊都是相等的,但只有 個(gè)角是相等的�����。
這個(gè)例子告訴我們四邊形的四條邊的長(zhǎng)度不改 改變�����,這叫四邊形的不穩(wěn)定性�����。
四邊形的不穩(wěn)定性在生活
7�����、中既有好處也有害處��,
伸縮門(mén)就是利用了四邊形的不穩(wěn)定性��,一些建筑物就要防止四邊形的不穩(wěn)定性�,如下圖的木橋欄桿加些斜
條,就是為了防止四邊形的不穩(wěn)定性��。
三應(yīng)用遷 移���,鞏固提 高
例1 一個(gè)多 邊形的內(nèi)角 和等于它的 外角和的5 倍��,它是幾 邊形����? 解:設(shè)這個(gè)
多邊形是n邊形,則它的內(nèi)角和是(n —2) ? 180 �����,外角和等于360 ,
所以:(n —2) ? 180=5X 360
解得:n=12
答:這個(gè)多邊形是12邊形.
四課堂練習(xí)�����,鞏固提高
1 一個(gè)四邊形的每一個(gè)外角都等于 45o,這個(gè)四邊形是幾邊形���?它的每一個(gè)內(nèi)角等于多少度?
2正12邊形的每一個(gè)內(nèi)角等于多少度��?每一個(gè)外角等于多少度�?
3下圖是三個(gè)完全相同的正多邊形拼成的無(wú)縫隙不重疊的圖形的一部分���,這種多邊形是幾邊形���?
五反思小結(jié),拓展提高
這節(jié)課我們學(xué)習(xí)了什么��?
作業(yè) P 117---118 A 3.4 B 2.3
 《多邊形的內(nèi)角和與外角和》教學(xué)設(shè)計(jì)-04
《多邊形的內(nèi)角和與外角和》教學(xué)設(shè)計(jì)-04