《2018年中考數(shù)學(xué)專題復(fù)習(xí)訓(xùn)練 相交線與平行線》由會(huì)員分享�,可在線閱讀,更多相關(guān)《2018年中考數(shù)學(xué)專題復(fù)習(xí)訓(xùn)練 相交線與平行線(9頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1�����、中考復(fù)習(xí)專題訓(xùn)練 相交線與平行線
一�����、選擇題
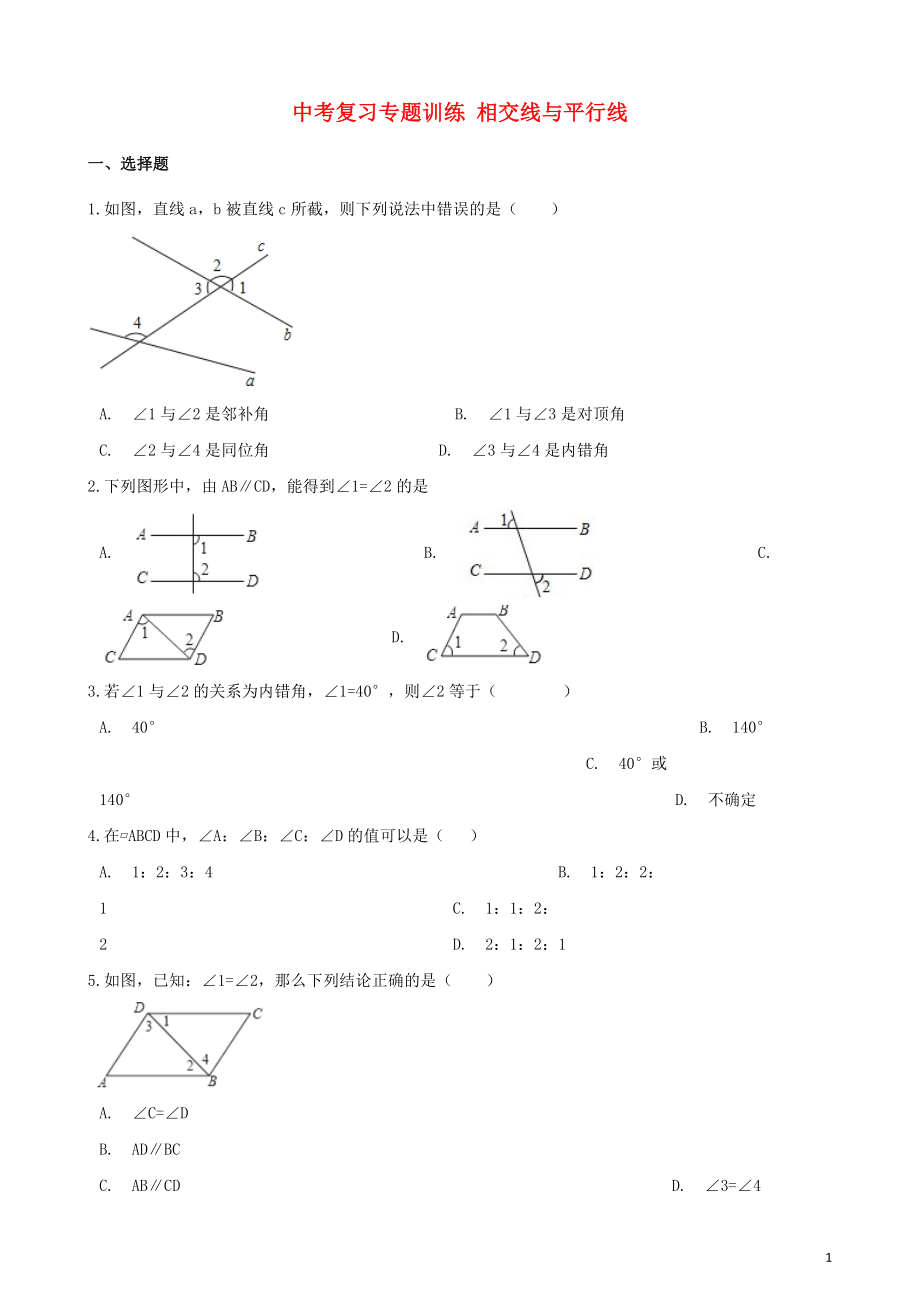
1.如圖�����,直線a��,b被直線c所截���,則下列說法中錯(cuò)誤的是( ?�。?
A.?∠1與∠2是鄰補(bǔ)角???????????B.?∠1與∠3是對(duì)頂角??????????C.?∠2與∠4是同位角??????????D.?∠3與∠4是內(nèi)錯(cuò)角
2.下列圖形中�,由AB∥CD��,能得到∠1=∠2的是
A.???????????B.???????????C.???????????D.?
3.若∠1與∠2的關(guān)系為內(nèi)錯(cuò)角���,∠1=40°,則∠2等于(????)
A.?40°??????????????????????
2��、???????????B.?140°?????????????????????????????????C.?40°或140°?????????????????????????????????D.?不確定
4.在?ABCD中�,∠A:∠B:∠C:∠D的值可以是(? )
A.?1:2:3:4?????????????????????B.?1:2:2:1?????????????????????C.?1:1:2:2?????????????????????D.?2:1:2:1
5.如圖,已知:∠1=∠2��,那么下列結(jié)論正確的是( ?�。?
A.?∠C=∠D????????
3����、??????????????????????B.?AD∥BC??????????????????????????????C.?AB∥CD??????????????????????????????D.?∠3=∠4
6.如圖,下列條件:∠1=∠2���;∠3=∠4�����;∠2+∠3=∠5���;∠2+∠3+∠A=180°��;∠4+∠1=∠5�����,能判定AB∥DC有( ?��。?
?
A.?3個(gè)???????????????????????????????????????B.?4個(gè)???????????????????????????????????????C.?5個(gè)???????????????
4、????????????????????????D.?6個(gè)
7.下列說法中��,正確的個(gè)數(shù)是( ?�。?
(1)同角的余角相等
(2)相等的角是對(duì)頂角
(3)在同一平面內(nèi)����,不相交的兩條直線叫平行線
(4)直線外一點(diǎn)與直線上各點(diǎn)連接的所有線段中,垂線段最短.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
8.如圖���,一條公路修
5�、到湖邊時(shí),需拐彎繞道而過��,如果第一次拐的角∠A是100°第二次拐的角∠B是150°����,第三次拐的角是∠C,這時(shí)的道路恰好和第一次拐彎之前的道路平行����,則∠C是(? )
A.?120°????????????????????????????????????B.?130°????????????????????????????????????C.?140°????????????????????????????????????D.?150°
9.(2017?東營(yíng))已知a∥b�����,一塊含30°角的直角三角板如圖所示放置�����,∠2=45°�,則∠1等于(?? )
A.?100°??????????
6、??????????????????????????B.?135°????????????????????????????????????C.?155°????????????????????????????????????D.?165°
10.(2017?南充)如圖����,直線a∥b,將一個(gè)直角三角尺按如圖所示的位置擺放�,若∠1=58°�����,則∠2的度數(shù)為(?? )
A.?30°???????????????????????????????????????B.?32°???????????????????????????????????????C.?42°?????????????????
7�����、??????????????????????D.?58°
11.如圖�,AB⊥AC�����,AD⊥BC���,那么點(diǎn)C到直線AD的距離是指???(??)
A.?線段AC的長(zhǎng)?????????????????????B.?線段AD的長(zhǎng)?????????????????????C.?線段DB的長(zhǎng)?????????????????????D.?線段CD的長(zhǎng)
12.如圖����,AB∥CD����,CE平分∠ACD,若∠1=25°���,那么∠2的度數(shù)是(?? )
A.?160°??????????????????????????????????????B.?50°???????????????????????????
8��、???????????C.?70°??????????????????????????????????????D.?60°
二��、填空題
13.如圖���,∠DAC與∠C是________?��,它們是直線________?和直線________?被直線________?所截而構(gòu)成的.
14.如圖����,給出下列條件:①∠1=∠2��;②∠3=∠4�;③AD∥BE���,且∠D=∠B�����;④AD∥BE�;且∠BAD=∠BCD.其中�����,能推出AB∥DC的條件為________.
15.已知如圖:AC⊥BC,CD⊥AB���,則點(diǎn)B到AC的距離是線段________?的長(zhǎng).
16.如圖�,∠1=80°����,∠2=100°,∠
9��、3=76°.則∠4的度數(shù)是________.
17.如圖�����,小島C在小島A的北偏東60°方向�,在小島B的北偏西45°方向,那么從C島看A����,B兩島的視角∠ACB的度數(shù)為________.
?
18.如圖:PC∥AB,QC∥AB���,則點(diǎn)P���、C�、Q在一條直線上.
理由是:________?
19.如圖����,∠1=70°,∠2=130°�����,直線m平移后得到直線n ��, 則∠3=________°.
20. 如圖���,一個(gè)含有30°角的直角三角形的兩個(gè)頂點(diǎn)放在一個(gè)矩形的對(duì)邊上��,若∠1=25°����,則∠2=________.
21.如圖�����,長(zhǎng)方形紙片ABCD沿EF折疊后�,ED交BC于點(diǎn)G,點(diǎn)
10���、D,C分別落在點(diǎn)D’����、C’位置上����,若∠EFG=55°,∠BGE=________度.
三�����、解答題
22.如圖所示�����,已知AB∥DC��,AE平分∠BAD�����,CD與AE相交于點(diǎn)F�,∠CFE=∠E�����,試說明AD∥BC.
23.如圖所示����,現(xiàn)有下列4個(gè)亊項(xiàng):(1)∠1=∠2�,(2)∠3=∠B,(3)FG⊥AB于G�����,(4)CD⊥AB于D.
以上述4個(gè)事項(xiàng)中的(1)����、(2)、(3)三個(gè)作為一個(gè)命題的己知條件����,(4)作為該命題的結(jié)論,可以組成一個(gè)真命題.請(qǐng)你證明這個(gè)真命題.
24.如圖�,點(diǎn)D,F(xiàn)在線段AB上�����,點(diǎn)E�����,G分別
11����、在線段BC和AC上,CD∥EF���,∠1=∠2.
(1)判斷DG與BC的位置關(guān)系����,并說明理由��;
(2)若DG是∠ADC的平分線���,∠3=85°�,且∠DCE:∠DCG=9:10����,試說明AB與CD有怎樣的位置關(guān)系?
25.如圖����,已知直線AB∥DF�����,∠D+∠B=180°��,
(1)求證:DE∥BC�����;
(2)如果∠AMD=75°�����,求∠AGC的度數(shù).
參考與答案
一�、選擇題
D B D D C A C B D B D B
二����、填空題
13. 內(nèi)錯(cuò)角;BD���;BC����;AC
14.
12、 ②③④
15. BC
16. 76°
17. 105°
18. 過直線外一點(diǎn)有且只有一條直線和已知直線平行
19. 20°
20. 115°
21. 110
三����、解答題
22. 解:∵AB∥CD�, ∴∠BAE=∠CFE,
∵AE平分∠BAD��,
∴∠BAE=∠DAF��,
∵∠CFE=∠E���,
∴∠DAF=∠E���,
∴AD∥BC
23. 證明:∵∠3=∠B,
∴DE∥BC����,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD���,
∴GF∥CD����,
∴∠CDB=∠BGF.
∵FG⊥AB,
∴∠BGF=90°����,
∴∠C
13、DB=90°��,
∴CD⊥AB.
24. (1)解:DG∥BC. 理由:∵CD∥EF��,
∴∠2=∠BCD.
∵∠1=∠2�,
∴∠1=∠BCD,
∴DG∥BC
(2)解:CD⊥AB. 理由:∵由(1)知DG∥BC��,∠3=85°���,
∴∠BCG=180°﹣85°=95°.
∵∠DCE:∠DCG=9:10���,
∴∠DCE=95°× =45°.
∵DG是∠ADC的平分線,
∴∠ADC=2∠CDG=90°����,
∴CD⊥AB
25. (1)證明:∵AB∥DF, ∴∠D+∠BHD=180°��,
∵∠D+∠B=180°,
∴∠B=∠DHB��,
∴DE∥BC
(2)解:∵DE∥BC�����,∠AMD=75°���, ∴∠AGB=∠AMD=75°,
∴∠AGC=180°﹣∠AGB=180°﹣75°=105°
9
 2018年中考數(shù)學(xué)專題復(fù)習(xí)訓(xùn)練 相交線與平行線
2018年中考數(shù)學(xué)專題復(fù)習(xí)訓(xùn)練 相交線與平行線