《人教版 小學(xué)8年級(jí) 數(shù)學(xué)上冊(cè) 12.3角的平分線的性質(zhì)教案》由會(huì)員分享����,可在線閱讀,更多相關(guān)《人教版 小學(xué)8年級(jí) 數(shù)學(xué)上冊(cè) 12.3角的平分線的性質(zhì)教案(4頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1��、2019人教版初中數(shù)學(xué)精品教學(xué)資料
12.3 角的平分線的性質(zhì)
教學(xué)目標(biāo)
知識(shí)與技能
1.能夠利用三角形全等���,證明角平分線的性質(zhì)和判定.
2.會(huì)用尺規(guī)作已知角的平分線.
3.能利用角平分線性質(zhì)進(jìn)行簡(jiǎn)單的推理,解決一些實(shí)際問(wèn)題.
過(guò)程與方法
經(jīng)歷探索��、猜想�、證明的過(guò)程,進(jìn)一步發(fā)展學(xué)生的推理證明意識(shí)和能力.
情感態(tài)度價(jià)值觀
在探討作角的平分線的方法及角的平分線的性質(zhì)的過(guò)程中��,培養(yǎng)學(xué)生探究問(wèn)題的興趣��,增強(qiáng)解決問(wèn)題的信心����,獲得解決問(wèn)題的成功體驗(yàn),逐步培養(yǎng)學(xué)生的理性精神
教學(xué)重點(diǎn)
角平分線畫法�����、性質(zhì)和判定.
教學(xué)難點(diǎn)
角的平分線的性質(zhì)的探究
教學(xué)準(zhǔn)備
平分角的儀
2�、器(自制)三角尺、多媒體課件等.
教學(xué)過(guò)程(師生活動(dòng))
設(shè)計(jì)理念
創(chuàng)設(shè)情境����,導(dǎo)入新課
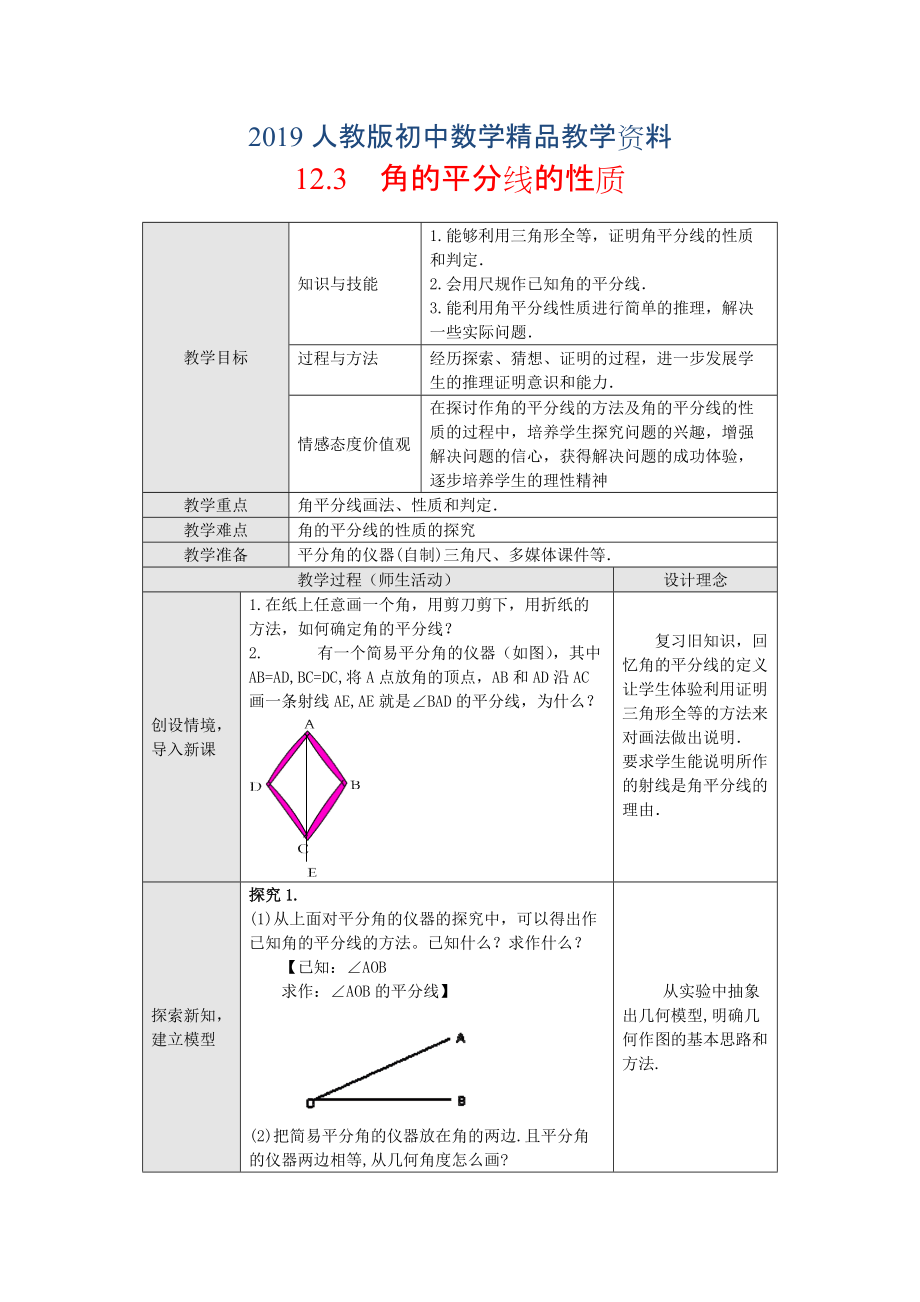
1.在紙上任意畫一個(gè)角����,用剪刀剪下���,用折紙的方法��,如何確定角的平分線?
2. 有一個(gè)簡(jiǎn)易平分角的儀器(如圖)�,其中AB=AD,BC=DC,將A點(diǎn)放角的頂點(diǎn),AB和AD沿AC畫一條射線AE,AE就是∠BAD的平分線���,為什么���?
復(fù)習(xí)舊知識(shí),回憶角的平分線的定義
讓學(xué)生體驗(yàn)利用證明三角形全等的方法來(lái)對(duì)畫法做出說(shuō)明.
要求學(xué)生能說(shuō)明所作的射線是角平分線的理由.
探索新知���,建立模型
探究1.
(1)從上面對(duì)平分角的儀器的探究中�,可以得出作已知角的平分線的方法���。已知什么�?求作什么���?
【已知
3����、:∠AOB
求作:∠AOB的平分線】
(2)把簡(jiǎn)易平分角的儀器放在角的兩邊.且平分角的儀器兩邊相等,從幾何角度怎么畫?
【以點(diǎn)O為圓心,適當(dāng)長(zhǎng)為半徑畫弧���,交OA于點(diǎn)M��,交OB于點(diǎn)N.】
(3) 簡(jiǎn)易平分角的儀器BC=DC,從幾何角度如何畫
【分別以點(diǎn)M����,N為圓心�,大于二分之一MN長(zhǎng)為半徑畫弧,兩弧在角的內(nèi)部交于點(diǎn)C.
(4)OC與簡(jiǎn)易平分角的儀器中,AE是同一條射線嗎?
【是】
(5)你能說(shuō)明OC是∠AOB的平分線嗎?
【提示:利用全等的性質(zhì)】
探究2.
(1)在已畫好的角的平分線OC上任意找一點(diǎn)P,過(guò)P點(diǎn)分別作OA��、OB的垂
4�����、線交OA����、O于M、N, PM���、PN的長(zhǎng)度是∠AOB的平分線上一點(diǎn)到∠AOB兩邊的距離��。量出它們的長(zhǎng)度��,你發(fā)現(xiàn)了什么���?
【多媒體課件動(dòng)態(tài)演示(可用“幾何畫板”制作)�����,當(dāng)拖動(dòng)∠AOB平分線OC上的點(diǎn)P時(shí),觀察PM����、PN(PM⊥OA,PN⊥OB)度量值的變化規(guī)律.
探究結(jié)果后可得到:PM⊥OA��,PN⊥OB����,且PM=PN】
(2)你能歸納角的平分線的性質(zhì)嗎?
【角的平分線上的點(diǎn)到角的兩邊的距離相等】
(3)你能用三角形全等證明這個(gè)性質(zhì)嗎?
探究3.
那么若一個(gè)點(diǎn)到角兩邊的距離相等,這個(gè)點(diǎn)是否在這個(gè)角的平分線上呢����?
如圖�,已知PD⊥OA,PE⊥OB,且PD
5�����、=PE�,那么P點(diǎn)在∠AOB的平分線上嗎?為什么��?
歸納:
角的內(nèi)部到角的兩邊的距離相等的點(diǎn)在這個(gè)角的平分線上.
從實(shí)驗(yàn)中抽象出幾何模型,明確幾何作圖的基本思路和方法.
培養(yǎng)學(xué)生運(yùn)用直尺和圓規(guī)作已知角的平分線的能力.
讓學(xué)生體驗(yàn)成功
在已有成功經(jīng)驗(yàn)的基礎(chǔ)上����,繼續(xù)探究與應(yīng)用,提升分析解決問(wèn)題的能力并增進(jìn)運(yùn)用數(shù)學(xué)的情感體驗(yàn).
在說(shuō)理的過(guò)程中加深對(duì)角平分線性質(zhì)�、判定定理的理解.
解析、
6����、應(yīng)用與拓展
思考:
如圖所示,要在S區(qū)建一個(gè)集貿(mào)市場(chǎng)���,使它到公路���、鐵路距離相等,離公路與鐵路交叉處500m,這個(gè)集貿(mào)市場(chǎng)應(yīng)建于何處(在圖上標(biāo)出它的位置����,比例尺為1:20000)?
問(wèn)題1.集貿(mào)市場(chǎng)建于何處��,和本節(jié)學(xué)的角平分線性質(zhì)有關(guān)嗎�?用哪一個(gè)性質(zhì)可以解決這個(gè)問(wèn)題?
2.比例尺為1:20000是什么意思��?
結(jié)論:
1.應(yīng)該是用第二個(gè)性質(zhì).這個(gè)集貿(mào)市場(chǎng)應(yīng)該建在公路與鐵路形成的角的平分線上����,并且要求離角的頂點(diǎn)500米處.
2.圖中1cm表示實(shí)際距離200m的意思.
作圖如下:
第一步:作∠AOB的平分線OP.
第二步:在射線OP上截取OC=2.5cm,確定C點(diǎn)�,C點(diǎn)就
7�、是集貿(mào)市場(chǎng)所建地了.
例題講解:
如圖,△ABC的角平分線BM��、CN相交于點(diǎn)P.
求證:點(diǎn)P到三邊AB�����、BC���、CA的距離相等.
分析:點(diǎn)P到AB��、BC���、CA的垂線段PD��、PE�、PF的長(zhǎng)就是P點(diǎn)到三邊的距離����,也就是說(shuō)要證:PD=PE=PF.而B(niǎo)M、CN分別是∠B�����、∠C的平分線����,根據(jù)角平分線性質(zhì)和等式的傳遞性可以解決這個(gè)問(wèn)題.
鞏固練習(xí)教材50頁(yè)練習(xí)1,2
發(fā)展學(xué)生應(yīng)用數(shù)學(xué)的意識(shí)與能力
只要作法合理,均應(yīng)給予肯定.
小結(jié)與作業(yè)
小結(jié)提高
我們學(xué)習(xí)了關(guān)于角平分線的兩個(gè)性質(zhì):
①角平分線上的點(diǎn)到角的兩邊的距離相等���;
②角的內(nèi)部到角的兩邊距離相等的點(diǎn)在角的平分線上.它們具有互逆性.
與角平分線有關(guān)的求證線段相等����、角相等問(wèn)題,可以直接利用角平分線的性質(zhì)��,而不必再去證明三角形全等來(lái)得出線段相等.
通過(guò)小結(jié)歸納���,完善學(xué)生對(duì)知識(shí)的梳理.
布置作業(yè)
1.必做題:
2.選做題:
本題是對(duì)所學(xué)內(nèi)容的復(fù)習(xí)����,又為下節(jié)課學(xué)習(xí)做準(zhǔn)備.
 人教版 小學(xué)8年級(jí) 數(shù)學(xué)上冊(cè) 12.3角的平分線的性質(zhì)教案
人教版 小學(xué)8年級(jí) 數(shù)學(xué)上冊(cè) 12.3角的平分線的性質(zhì)教案